CIRCUIT DE LOGIQUE COMBINATOIRE

Comment appliquer la logique combinatoire pour résoudre et simplifier des problèmes d’automatisation.

Sans plus tarder, en voici un exemple. Vous êtes chargé de réaliser un système de votation tout simple. Lors des réunions d’un conseil d’administration, composé de trois membres, les décisions sont prises à la majorité. Vous devez donc réaliser un circuit de logique combinatoire qui fera en sorte qu’une lampe s’allume lorsque la majorité est atteinte. Chacun des trois membres du conseil vote en appuyant sur un interrupteur lorsqu’il est d’accord avec le projet soumis au vote.

Identification des variables d’entrée et de sortie

Quelles sont les variables d’entrée du système de votation selon l’énoncé du problème ? On trouve trois variables d’entrée, une pour chaque interrupteur utilisé par un membre du conseil pour voter. Chacun des interrupteurs détermine l’état d’une des trois entrées du circuit: «1» lorsque l’interrupteur est actionné et «0» lorsqu’il ne l’est pas. Ces variables d’entrée seront désignées par les lettres majuscules «A», «B» et «C». Quant au nombre de variables de sortie, il n’y en a qu’une: elle correspond à la lampe qui s’allume ou non selon l’issue du vote. Cette sortie sera désignée par un «S».

Construction de la table de vérité

Vous avez vu des exemples de tables de vérité pour les opérateurs logiques de base. La table de vérité est une compilation, sous forme de tableau, de tous les états logiques de la sortie en fonction des états logiques des entrées. Les étapes à suivre pour construire une table de vérité sont les suivantes:

Écrivez, sur une première ligne, le nom des variables d’entrée et celui de la variable de sortie.
Divisez le tableau en un nombre de colonnes égal au total des entrées et de la sortie. Ainsi, la table de vérité d’une fonction logique à deux entrées aura trois colonnes (deux pour les entrées et une pour la sortie).
Déterminez le nombre de combinaisons possibles à l’aide des variables d’entrée. Ce nombre est égal à 2 exposant le nombre d’entrées. Par exemple, avec trois entrées, il y aura 23 = 8 combinaisons possibles.
Tracez des lignes horizontales en un nombre égal au nombre de combinaisons possibles. Chaque ligne correspond à une combinaison unique des variables d’entrée.
Remplissez chaque ligne par une combinaison de variables d’entrée. La meilleure façon d’énumérer toutes les combinaisons possibles sans se tromper est de compter en binaire.
Inscrivez, dans la colonne «Sortie», la valeur de la fonction pour chaque combinaison.

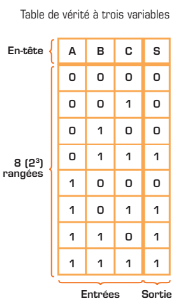
Comme la table de vérité du système de votation compte trois variables d’entrée, elle se présentera comme suit:

quatre colonnes (trois entrées et une sortie);
huit rangées (23 combinaisons d’entrées) et une de plus pour identifier les variables en en-tête.

Les combinaisons de variables d’entrée correspondent à l’ordre de comptage binaire dans une table de vérité. Au bout de chaque combinaison, l’état logique de la sortie correspondante est inscrit dans la colonne «Sortie». Dans le cas du système de votation, la lampe doit s’allumer (sortie à «1») lorsque deux ou trois membres du conseil actionnent leurs interrupteurs (entrée à «1»). Par conséquent, quatre sorties sur huit donneront un «1».

Formulation de l’équation logique

Comment tirer une équation logique d’une table de vérité ? Il existe deux façons de faire: la somme de produits (S.O.P., Sum of Products) et le produit de sommes (P.O.S., Product of Sums).

Somme de produits

Selon cette forme d’équation logique, on écrit chacune des lignes de la table de vérité dont la sortie est «1» comme un produit logique ET. Ensuite, chaque partie d’équation est réunie en une somme logique OU. On doit aussi tenir compte de l’état des variables: si la variable d’entrée est un «1», elle est remplacée par son nom, tandis que si son état est un «0», on la remplace par sa négation. Cette méthode est avantageuse lorsque la table de vérité compte une minorité de sorties à l’état «1».

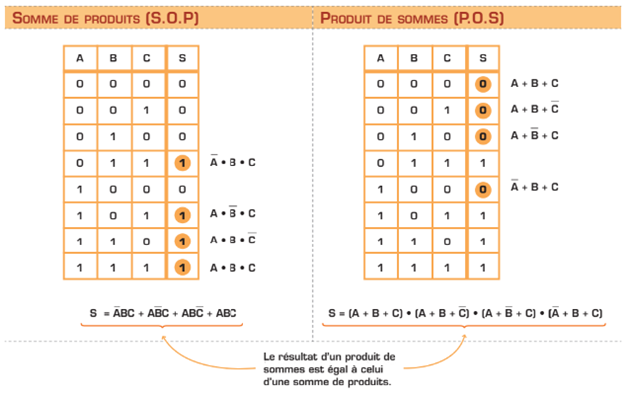
Produit de sommes

Cette deuxième forme consiste à écrire chacune des lignes de la table de vérité dont la sortie est «0» comme une somme logique OU. Les parties d’équation ainsi obtenues peuvent alors être réunies selon un produit logique ET. Les variables d’entrée à l’état logique «0» sont remplacées par leur nom, tandis qu’on ajoute une barre à celles dont l’état logique est «1». On a recours à la forme P.O.S. lorsque la table de vérité compte une minorité de sorties à l’état «0».

Dans l’exemple du système de votation, on remarque que la moitié des combinaisons d’entrées possibles (quatre sur huit) correspond à une sortie à l’état «1». Par conséquent, l’une ou l’autre des deux formes d’équation, S.O.P. ou P.O.S., aboutit à une équation comportant quatre blocs. Retenez que le résultat d’un produit de sommes est égal à celui d’une somme de produits.

Schématisation d’un circuit à partir d’une équation logique

Afin de pouvoir réaliser le circuit logique du système de votation, il faut maintenant traduire en schéma logique l’une ou l’autre des équations obtenues. Prenez l’équation trouvée à partir de la méthode S.O.P., par exemple:

Pour construire le schéma logique correspondant à cette équation, vous aurez besoin de quatre portes logiques ET à trois entrées, trois portes NON (inverseurs) et d’une porte OU à quatre entrées.

Si un système de votation relativement simple emploie des portes logiques à trois et à quatre entrées, de quoi seront constitués les automatismes plus complexes? Afin d’éliminer tout composant inutile et ainsi rendre le circuit logique plus efficace et facile à comprendre, il vaudra mieux simplifier l’équation logique.

Simplification à l’aide de l’algèbre booléenne

Vous connaissez déjà les opérateurs logiques booléens ET, OU et NON. Vous êtes même convaincu de leur utilité pour combiner les variables d’un circuit logique. Quant à l’algèbre booléenne, elle vous sera utile pour simplifier des équations grâce à un ensemble de postulats, de théorèmes et de lois.

Postulats de l’algèbre booléenne

Un postulat est un fait reconnu, établi. Il ne comporte que des constantes. Le tableau suivant dresse une liste des postulats de l’algèbre de Boole (P1 à P8). Chaque postulat y est représenté par un circuit électrique et un schéma logique. Le symbole de la lampe à la sortie de chaque circuit rend compte du résultat à la sortie pour chacun des postulats. Comme vous le voyez, ces postulats peuvent être matérialisés et vérifiés au moyen de portes logiques.

Théorèmes et lois de l’algèbre booléenne

Un théorème est un énoncé qu’on peut démontrer sur la base de ce qui est établi. Il ne comporte qu’une seule variable. Le théorème est donc énoncé à partir d’une seule variable booléenne qu’on place en présence des opérateurs logiques ET, OU et NON. Le tableau suivant énumère les théorèmes de l’algèbre de Boole ; ceux-ci sont accompagnés de leur preuve et de leur table de vérité.

Les lois de l’algèbre de Boole s’appliquent à plusieurs variables à la fois. Ces lois permettent de trouver des circuits équivalents qui, dans certains cas, sont beaucoup plus simples ou faciles à réaliser. Le tableau suivant répertorie l’ensemble de ces lois, accompagnées de leur représentation en portes logiques.

Exemple de simplification avec l’algèbre de Boole

La simplification s’effectue par étapes, en utilisant les théorèmes et les lois de l’algèbre de Boole. Prenez soin de noter chaque loi ou chaque théorème utilisé; ce sera plus facile ensuite de vérifier votre travail. La figure suivante montre un exemple de simplification. L’équation logique de départ est celle du système de votation, sous la forme d’une somme de produits.

Exemple de simplification d’une équation logique:

Examinez maintenant le schéma logique de l’équation simplifiée. Comme vous le voyez, la réduction du nombre de portes logiques et du nombre d’entrées de ces portes est appréciable.

Circuits équivalents

Par mesure d’économie ou pour simplifier les choses, vous aurez avantage à réduire le nombre de types de portes utilisées dans vos montages. Pour y arriver, vous devrez trouver des équivalences en utilisant les portes les plus populaires, soit les portes NON-OU (NOR) et NON-ET (NAND), qualifiées d’universelles, ainsi que la porte NON.

La plupart des portes logiques ont d’autres portes équivalentes, ou du moins, des symboles équivalents. Par exemple, la porte NON peut être remplacée par une porte NON-OU aux entrées reliées ensemble. Une autre possibilité consiste à remplacer l’inverseur par une porte NON-ET dont les entrées sont interreliées. On pourrait énumérer ainsi de nombreuses possibilités, mais il est plus simple de les résumer dans un tableau.

Dans le but de faciliter la compréhension des circuits, on trace parfois le schéma du montage à l’aide de symboles équivalents. Ces symboles équivalents reposent sur le principe des lois de De Morgan. On procède à cette conversion en deux étapes:

inversion de la porte logique (un ET devient un OU et vice-versa);
inversion des signaux d’entrée et de sortie (retrait des cercles là où il y en a et ajout dans le cas contraire).

Prenez l’exemple du circuit logique de la figure suivante, qui requiert trois circuits intégrés différents.

Ce circuit peut être modifié de manière à n’utiliser qu’un seul type de porte logique, soit la porte NON-ET (partie A). À première vue, la fonction de sortie semble différente. Cependant, le circuit tracé à l’aide du symbole équivalent de la porte NON-ET simplifie l’analyse du fonctionnement. Lorsque deux petits cercles (indiquant le niveau bas) sont présents à chaque extrémité d’un signal, ils s’annulent. C’est ainsi que, dans la partie B de la même figure, le signal entre les deux portes devient tout simplement AB.

Comme le montre cet exemple, l’usage de portes NON-ET réduit le nombre de C.I. à un seul comparativement à trois pour le même circuit réalisé à l’aide de portes conventionnelles ET, OU et NON. De ce fait, on diminue considérablement l’espace nécessaire au montage ainsi que son coût.

Simplification à l’aide du tableau de Karnaugh

Comme vous avez pu le constater, pour simplifier une équation logique à l’aide de l’algèbre booléenne, il faut en connaître les lois et les théorèmes. Il existe cependant une autre méthode de simplification : le tableau de Karnaugh (ou table de Karnaugh). Si le tableau de Karnaugh demande lui aussi un peu de réflexion, il a quand même le mérite d’être plus graphique.

Caractéristiques d’un tableau de Karnaugh Le tableau de Karnaugh est une grille dont le nombre de cases est en fonction du nombre de variables d’entrée. En effet, ce nombre correspond à 2, élevé à l’exposant du nombre de variables d’entrée. Ainsi, par exemple, s’il y a trois variables d'entrée, le tableau comptera 2(exp)3 cases, soit 8 cases.

Les diverses combinaisons possibles sont placées dans un ordre bien précis dans un tableau de Karnaugh. Étant donné qu’une seule variable ne doit pas changer d’état pour deux cases adjacentes, on utilise le code Gray au lieu du code binaire.

Transposition dans un tableau de Karnaugh

Pour remplir un tableau de Karnaugh à partir d’une table de vérité, il suffit d’inscrire l’état de chacune des sorties de la table de vérité dans la bonne case du tableau de Karnaugh.

Comme vous pouvez le voir, le tableau de Karnaugh occupe beaucoup moins d’espace que la table de vérité ; ce qui indique qu’on progresse vers une simplification de l’équation. Assurez-vous de transcrire l’état de chaque sortie de la table de vérité dans la bonne case du tableau. Pour vous faciliter la tâche, numérotez préalablement chacune des cases du tableau de Karnaugh.

Règles de regroupement

La disposition des combinaisons dans un tableau de Karnaugh respecte un ordre précis où intervient la notion des cases «adjacentes». On dit que deux cases sont adjacentes lorsqu’elles sont situées côte à côte, que ce soit à l’horizontale ou à la verticale. De plus, lorsque deux cases sont dites adjacentes dans un tableau de Karnaugh, une seule variable change d’état d’une case à l’autre.

Un point qui n’est pas évident de prime abord est le fait que les cases de la ligne supérieure du tableau peuvent être adjacentes à celles de la ligne inférieure. Il en est de même pour les cases du côté gauche et celles du côté droit. Pour l’admettre, il faut voir «s’enrouler» le tableau de Karnaugh sur le plan horizontal ou vertical.

Le regroupement des cases adjacentes permet de réduire une équation logique à sa version la plus simple. Il doit se faire en respectant certaines règles afin que l’équation ainsi obtenue corresponde bien aux données du problème. Les règles de regroupement sont les suivantes:

Regroupez les cases adjacentes, mais seulement celles qui présentent la même valeur : des «1», sinon des «0». En général, on regroupe les «1».
Repérez les plus grands groupes de cases de même valeur d’abord, puis terminez par les cases uniques. Vous éviterez ainsi les groupements inutiles.
Retenez que le nombre de cases adjacentes d’un groupement doit toujours être égal à une puissance de deux (2n): 2e0, 2e1, 2e2, 2e3… soit 1, 2, 4, 8 cases, etc.
Effectuez des groupements symétriques : les cases adjacentes de même valeur pourront donc former une ligne, un carré ou un rectangle.
Pensez à regrouper par enroulement les cases de même valeur situées de part et d’autre du tableau : la colonne de droite avec celle de gauche ainsi que la ligne du haut avec celle du bas.
Sachez qu’il est possible de regrouper des cases de même valeur situées aux quatre coins d’un tableau de Karnaugh, car elles sont adjacentes par enroulement dans les deux sens.

Notez que les groupements peuvent se chevaucher de sorte qu’une case pourra appartenir à plusieurs groupes.

Conversion des groupements en équation logique

Chaque groupement effectué dans un tableau de Karnaugh constitue une partie de l’équation logique finale. On commence généralement par écrire l’équation avec les groupements les plus grands pour finir par les plus petits et les cases uniques.

La façon de lire les groupements est simple: il suffit de repérer les variables qui ne changent pas d’état d’une case à l’autre à l’intérieur du périmètre d’un groupement. Ce sont ces variables qui feront partie de l’équation sous la forme d’un produit logique ET. Dans le cas où l’on a plus d’un groupement, on sépare chacune des parties de l’équation par une addition logique OU. Un premier exemple de conversion vous est proposé dans la figure suivante. Analysez un à un chacun des groupements

L’équation finale sera obtenue par la somme de tous les produits (forme S.O.P.) provenant des divers groupements : S = C ∙ D + B ∙ C + A ∙ B ∙ C ∙ D.

Voici un deuxième exemple de conversion où le produit résultant pour chaque groupement vous est donné ainsi que l’équation logique finale. Au besoin, retournez voir les explications qui précèdent.

La simplification, à l’aide de l’algèbre booléenne ou d’un tableau de Karnaugh, a pour but de rendre le montage final aussi simple que possible. Ce dernier comportera donc moins de pièces, occupera moins d’espace et coûtera moins cher. En outre, un montage simple est nettement plus facile à vérifier et à dépanner.

Représentation de l’exclusivité OU

Vous avez vu antérieurement les portes OU et NON-OU exclusifs. Ces deux types de porte n’apparaissent pas directement lors de la simplification à l’aide du tableau de Karnaugh. On travaillera donc avec des équivalences logiques pour l’utilisation de ces deux portes exclusives.

En observant les quelques exemples de tableaux de Karnaugh de la figure suivante, on remarque qu’une fonction exclusive possède des valeurs réfléchies (valeurs contraires) de part et d’autre de l’axe central.

États indéterminés ou indifférents à la sortie

Il peut arriver que la définition d’un problème ne permette pas de déterminer la valeur de la sortie pour chacune des combinaisons. On dit alors que la sortie reste indéterminée. Dans d’autres situations, certaines conditions d’entrée n’ont aucune influence sur le résultat de la sortie. On appelle ces conditions des états indifférents. En ce qui concerne la table de vérité, on identifiera les sorties indéterminées ou indifférentes à l’aide du symbole «Ø». Notez que le symbole «X» est parfois utilisé pour les identifier.

Que faire devant de telles sorties indéterminées ou indifférentes? Quelques options s’offrent à vous selon la situation. Il faut d’abord déterminer s’il n’est pas préférable, pour des raisons de sécurité, de choisir le niveau de sortie. Par exemple, si deux sorties actionnent un moteur, l’une dans le sens horaire et l’autre dans le sens antihoraire, et que l’état de chacune de ces sorties est indéterminé, alors un choix sécuritaire s’impose. Ainsi, pour éviter de commander en même temps deux actions qui s’opposent, on choisit un niveau bas (0) pour chaque sortie. L’autre option consiste à choisir une valeur de sortie qui permettra de réduire le nombre de groupements dans le tableau de Karnaugh. Ce choix pourra simplifier du coup l’équation, puis le montage. Bien sûr, cette modification ne doit pas nuire à la sécurité du système. La figure suivante présente deux tableaux de Karnaugh dans lesquels on a dû choisir le niveau d’une sortie indéterminée.

Relais programmable

Lorsque vient le temps de matérialiser un circuit logique, l’utilisation d’un relais programmable est simple et efficace. En effet, ce proche parent de l’automate programmable industriel vous évitera d’avoir à monter des circuits intégrés sur une plaque d’essai. Le relais programmable contient des centaines de portes logiques dont on peut programmer les interconnexions. Il contient aussi un bon nombre de composants utiles en logique séquentielle tels que des temporisateurs, des minuteries, des bascules et des compteurs.

Pour des applications simples d’automatisation, qui n’impliquent qu’un nombre restreint d’entrées et de sorties, de l’ordre d’une dizaine, par exemple, il ne serait pas justifié d’utiliser un automate programmable industriel. Par contre, le relais programmable (ou contrôleur logique) serait un bon choix.

Cette technologie présente plusieurs avantages:

Occupe peu d’espace.
Coûte bien moins cher qu’un véritable automate programmable. Est relativement simple à installer et à programmer.
Propose des fonctions intégrées (temporisateur, compteur, etc.) en plus des fonctions logiques de base (NON, ET, OU).
Est facilement reprogrammable.
La saisie du programme peut s’effectuer depuis un PC connecté au relais programmable ou directement par l’interface touches-afficheur de ce dernier.

Le relais programmable sert d’interface entre les capteurs qui alimentent les entrées du circuit à programmer (boutons-poussoirs, détecteurs, etc.) et ses sorties (lampes, contacteurs, etc.). La figure de la page suivante illustre quelques-uns des branchements possibles à réaliser avec un relais programmable.

Avant d’utiliser un relais programmable, prenez toujours connaissance de son manuel d’utilisation. Vous y trouverez les spécifications techniques de l’appareil, notamment les tensions et courants limites de ses entrées et sorties. Procurez-vous un relais programmable et son manuel d’utilisation afin de constater par vous-même toute l’information utile qu’il contient concernant le câblage.

Le relais programmable est fourni avec un logiciel qui permet de le programmer à partir d’un PC. Pour tester le programme, ce logiciel de programmation peut être utilisé en mode simulation. Vous pouvez donc observer comment se comportent les sorties en fonction de l’état des entrées. Il est également possible d’apporter des modifications au programme, au besoin, sans que le relais programmable soit branché aux composants extérieurs.