FONCTIONS LOGIQUES COMBINATOIRES
De quoi est composé un circuit de logique combinatoire? Y a-t-il une façon particulière de le schématiser? Comment fait-on pour matérialiser un tel circuit et vérifier s’il fonctionne bien? Vous obtiendrez des réponses à ces questions dans cette section.
Systèmes de numération et de codage
Il vous arrive sans doute, à vous aussi, de compter sur vos dix doigts. Ce n’est donc pas un hasard si le système de numération le plus répandu comporte dix symboles de notation. Si la tendance se maintient, le système de numération décimale, celui que vous utilisez sans trop y penser, est là pour de bon. Sachez cependant qu’il en existe d’autres qui pourront vous être utiles en électricité: les systèmes de numération binaire et hexadécimale. Dans cette section, vous verrez donc la notation de ces systèmes de numération et la façon de convertir un nombre d’un système à l’autre. Enfin, vous aurez à vous familiariser avec les systèmes de codage les plus populaires: DCB et Gray.
Système décimal
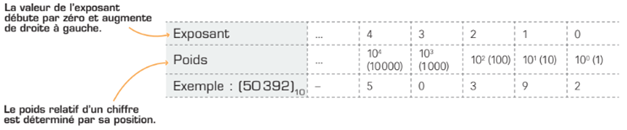
Comme son nom l’indique, le système décimal comprend dix symboles de numération, soit les chiffres de 0 à 9 inclusivement. Notez que le nombre de chiffres d’un système de numération constitue sa base. Ainsi, on dira d’un nombre décimal qu’il est en base 10. Le poids de chaque chiffre d’un nombre entier, ou sa valeur, est déterminé par sa position relative. Le poids d’un chiffre augmente de la droite vers la gauche. Ainsi, dans la base 10, vous trouverez toujours dans le même ordre croissant: les unités (1 = 10E0), les dizaines (10 = 10E1), les centaines (100 = 10E2), les milliers (1000 = 10E3), etc. La valeur de l’exposant augmente donc de droite à gauche en partant de zéro.
Systèmes binaire, octal et hexadécimal
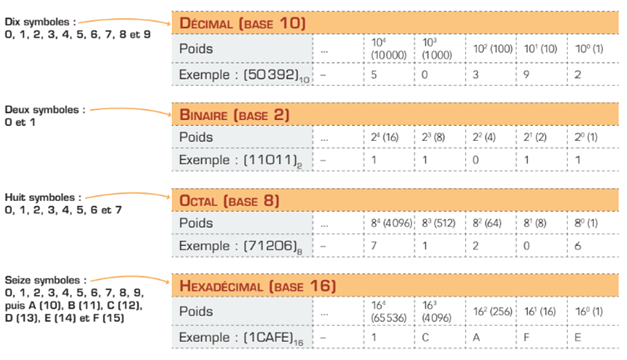
Tous les systèmes de numération sont construits de façon semblable. Qu’un nombre soit en base 10 (décimal), en base 2 (binaire), en base 16 (hexadécimal) ou en toute autre base numérique de votre choix, le chiffre qui identifie sa base indique le nombre de ses symboles de numération. Combien de symboles le système binaire comprend-il? La réponse est deux. Quant aux autres systèmes de numération, l’octal et l’hexadécimal (bases huit et seize), ils disposent respectivement de huit et de seize symboles de numération. Comparez les systèmes de numération entre eux de manière à identifier leurs points communs et leurs différences. Dans tous ces systèmes de numération, la valeur de l’exposant débute par zéro et augmente de droite à gauche. De plus, le poids relatif d’un chiffre, c’est à dire son importance, est déterminé par sa position
Lorsqu’on travaille avec différentes bases, on doit pouvoir les différencier. Pour ce faire, on place généralement le nombre entre parenthèses, puis on ajoute le chiffre identifiant la base en indice, par exemple: (10011)2.
Conversion vers le système décimal
Vous trouverez l’équivalent décimal d’un nombre binaire, octal ou hexadécimal, de la manière suivante:
- multipliez chaque chiffre du nombre par son poids relatif;
- additionnez ensuite tous les produits partiels obtenus.
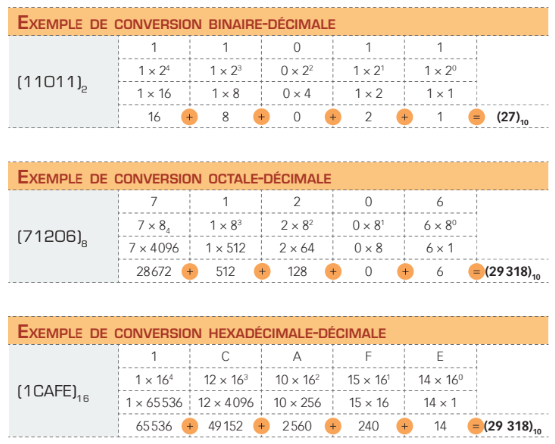
Conversion du système décimal à un autre système
La conversion du système décimal à un autre système de numération s’effectue par une série de divisions.
Nombre décimal vers nombre binaire
La conversion d’un nombre décimal en nombre binaire se réalise en effectuant des divisions successives par deux jusqu’à l’obtention d’un résultat (ou quotient) de 0 avec un reste de 1.
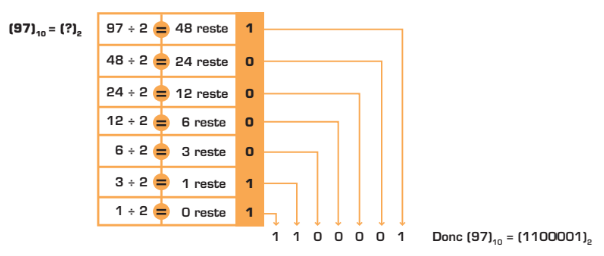
Remarquez que l’avant-dernière division (3 ÷ 2) donne un quotient de 1, lequel, divisé par deux, donne 0 comme quotient et 1 comme reste. La conversion est alors terminée.
Nombre décimal vers nombre octal
Cette conversion consiste à transformer le nombre décimal en effectuant une suite de divisions par huit. Le reste de la première division donne le chiffre du poids le plus faible, soit 80. Le résultat, ou quotient, est quant à lui divisé de nouveau par huit. L’opération se termine lorsqu’on obtient un quotient de 0; le reste correspond alors au chiffre du poids le plus fort.
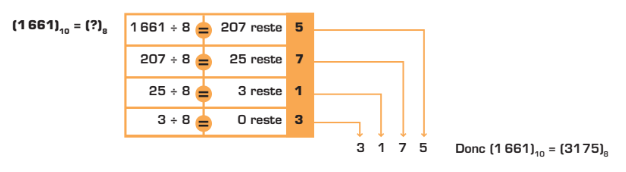
Nombre décimal vers nombre hexadécimal
Pour convertir un nombre décimal en un nombre hexadécimal, vous devez le diviser successivement par seize jusqu’à ce que le quotient soit de 0. Le reste de ces divisions successives est, à chaque étape, reporté comme étant un chiffre du nombre hexadécimal en commençant par le poids le plus faible comme présenté à la page suivante.

Conversion entre les systèmes binaire et octal
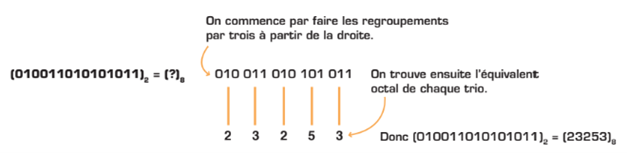
La conversion est simple: il suffit de réunir les chiffres binaires par groupes de trois. Le tableau ci-contre montre les équivalences entre les groupements binaires et les chiffres octaux. L’utilisation de ce tableau permet une conversion directe. En effet, si on doit passer du système binaire au système octal, on groupe les chiffres du nombre binaire par lots de 3 bits, à partir de la droite. Chaque trio peut alors être représenté par son équivalent octal. Il arrive parfois que le dernier trio ne soit pas complet (il manque un ou deux chiffres). Dans ce cas, on doit le compléter en ajoutant un ou des zéros à gauche.

Conversion entre les systèmes binaire et hexadécimal
La conversion d’un nombre binaire en un nombre hexadécimal s’effectue en regroupant les bits du nombre binaire par quadruplets. Cette disposition permet un passage rapide du système binaire au système hexadécimal. Les groupements de bits sont effectués de la droite vers la gauche. Si le dernier groupe ne possède pas quatre chiffres, on le complète par des zéros. Chaque quadruplet ainsi formé correspond à un symbole hexadécimal. Binaire Octal 000 0 001 1 010 2 011 3 100 4 101 5 110 6 111

La conversion d’un nombre hexadécimal en un nombre binaire s’effectue en représentant chaque chiffre du nombre hexadécimal par son équivalent binaire de quatre bits. Il est important de savoir qu’on doit conserver le quadruplet entier, même si celui-ci débute par un ou des zéros. Ces derniers prennent toute leur importance lorsqu’on forme les séries de quatre bits.

Systèmes de codage
Jusqu’à maintenant, vous avez pu vous familiariser avec les systèmes de numération les plus courants. Permettent-ils de couvrir toutes les situations? Pas toutes. L’ajout des codes DCB et Gray est donc devenu nécessaire avec le temps. Ces deux systèmes de codage sont en quelque sorte des dérivés du système binaire, le système de numération le plus utilisé dans les circuits logiques.
Code DCB
Le code DCB ou décimal codé binaire (BCD, Binary Coded Decimal) permet de représenter les nombres décimaux par une numération binaire pondérée. On le rencontre principalement dans le décodeur DCB à sept segments, qui est un dispositif d’affichage numérique décimal. Il facilite donc l’échange d’information entre l’humain, qui travaille en décimal, et la machine, qui reconnaît strictement le binaire. Le code DCB ressemble un peu à la représentation binaire d’un nombre hexadécimal.
En effet, ce code se compose de séries de quatre bits ou quartets (nibbles). La différence réside dans le nombre de chiffres représentés qui, dans ce cas, se limite à dix (0 à 9). Le tableau ci-contre contient les équivalences du code DCB et des chiffres décimaux. Ce type de code peut, par exemple, être employé pour faire le lien entre un automate programmable et des roues encodeuses. Pour convertir un nombre décimal en code DCB, il suffit de chercher l’équivalent DCB de chaque chiffre.
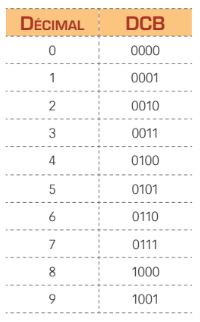

La conversion du code DCB en numération décimale s’obtient suivant le même raisonnement. Chaque groupe de quatre bits, de la droite vers la gauche, est converti en chiffre décimal.

Code Gray
Le code Gray est une autre forme de la base binaire. Sa principale caractéristique est qu’un seul bit change d’état lors de l’incrémentation, c’est- à-dire lorsqu’on passe d’un nombre au suivant. C’est pour cette raison que ce système de codage est très utilisé dans les convertisseurs analogiques- numériques. La conversion d’une valeur angulaire analogique (telle la position de l’axe d’un moteur) en une grandeur numérique nécessite un code dont les grandeurs successives ne diffèrent que d’un bit. Cela permet d’éviter des erreurs de détection. Par exemple, le passage du chiffre 3 au chiffre 4 nécessite un changement d’état des trois bits à la fois dans le système binaire ordinaire (0011 à 0100) au lieu de (0010 à 0110) dans le code Gray. Retenez que le code Gray ou «code binaire réfléchi» est également utile pour simplifier des circuits en logique combinatoire et séquentielle.
Le tableau suivant présente les équivalents du code Gray et des bases décimale et purement binaire.
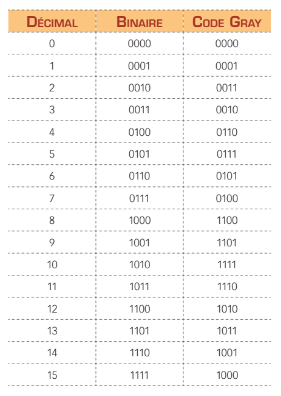
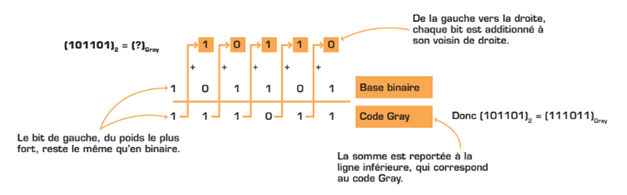
La conversion d’un nombre binaire en code Gray se fait tel qu’indiqué dans la figure ci-dessous. Comme vous pouvez le voir, les retenues sont négligées. De plus, le résultat en système binaire comporte toujours le même nombre de bits que la représentation en code Gray.
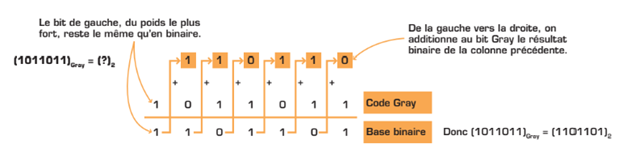
La conversion inverse, d’un nombre du code Gray en nombre binaire, ressemble légèrement à la précédente. Encore une fois, les retenues sont négligées et le résultat en binaire comporte toujours le même nombre de bits que son équivalent en code Gray.
Fonctions logiques combinatoires
Un circuit de logique combinatoire est composé d’un ensemble de fonctions logiques agencées de manière à faire fonctionner un automatisme qui n’a pas de mémoire. En d’autres mots, pour une combinaison d’entrées, il ne correspond qu’à une seule et unique sortie. On peut dire aussi du circuit de logique combinatoire qu’il est en boucle ouverte. Comme vous le verrez plus loin, le circuit de logique séquentielle comporte lui aussi un agencement de fonctions logiques. Par contre, il peut mémoriser de l’information et effectuer ainsi une séquence d’opérations selon un ordre précis.
La porte logique est l’élément de base à partir duquel sont construits les circuits de logique combinatoire. Il s’agit d’un circuit électronique comportant une ou plusieurs entrées et une seule sortie.
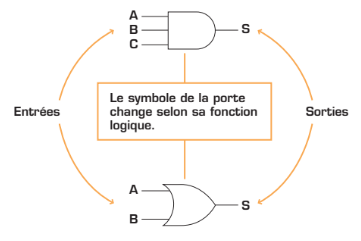
Tout circuit logique fonctionne selon un mode binaire. Par conséquent, les variables d’entrée ou de sortie, appelées aussi «variables logiques» ou «booléennes», ne prendront que l’une ou l’autre des deux valeurs possibles: «1» ou «0»; c’est tout ou rien. Selon le contexte, les deux états logiques pourraient être désignés par: haut ou bas, marche ou arrêt, ouvert ou fermé, vrai ou faux, oui ou non, etc.
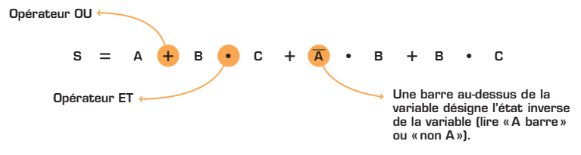
La porte logique exécute une opération logique sur l’état de ses entrées, puis l’état de sa sortie correspond au résultat de cette opération. Il existe une variété de portes logiques pouvant exécuter différentes opérations logiques. Les opérations effectuées par celles-ci peuvent être exprimées sous forme d’équations logiques. Ainsi, les variables d’entrée et de sortie sont mises en relation par des opérateurs logiques, qui s’apparentent aux opérateurs mathématiques (+, -, ×, ÷). En tout, trois opérateurs logiques de base, OU, ET, NON, suffisent pour décrire les relations entre les entrées et les sorties, et ce, pour n’importe quel circuit logique.
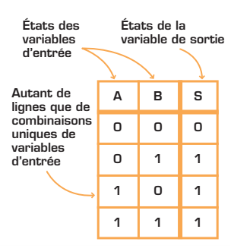
En logique combinatoire, chaque combinaison d’entrées correspond à une seule sortie. Afin de visualiser l’état des entrées et des sorties, on utilise une table de vérité. Il s’agit d’un tableau qui compte autant de lignes qu’il y a de combinaisons possibles de variables d’entrée.
Les variables utilisées dans les circuits logiques sont représentées par des lettres majuscules. Les variables d’entrée sont désignées par les premières lettres de l’alphabet (A, B, C…), tandis que les variables de sortie sont représentées par les dernières (S, T, U, V…).
Porte logique OU
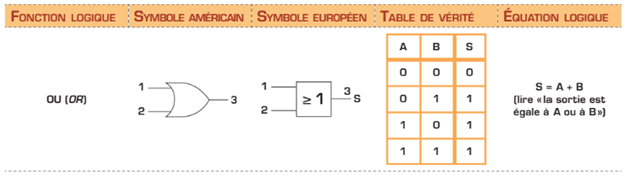
En logique, l’opération OU (en anglais, OR) se définit comme une addition (+). L’opérateur OU réalise l’opération suivante: si l’une ou l’autre des entrées est à l’état « 1 », l’état obtenu à la sortie est « 1 ». L’opération OU pourrait être représentée par un circuit électrique en parallèle. Dans un tel circuit, il faut qu’au moins un des interrupteurs soit actionné pour que la lampe s’allume.
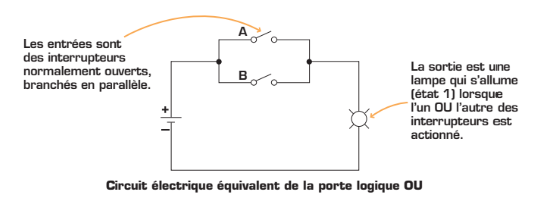
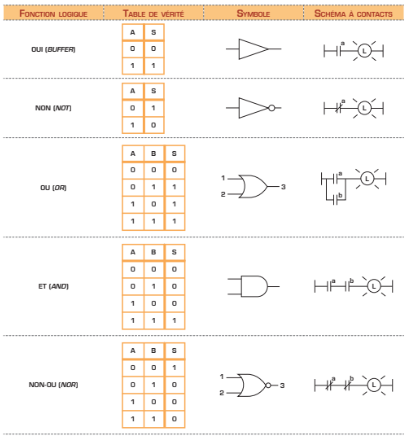
Pour réduire la complexité d’un schéma de circuit, et ainsi voir rapidement le fonctionnement de ce circuit, on utilise des symboles logiques et une table de vérité. C’est ainsi que la porte logique OU est présentée dans le tableau de la page suivante. Vous y trouverez également l’équation logique qui lui est associée. Dans la table de vérité de la porte logique OU, remarquez bien que la sortie est à l’état « 1 » chaque fois que l’une ou l’autre des entrées est à l’état « 1 ».
Porte logique ET
En logique, l’opération ET (en anglais, AND) se définit comme étant la multiplication (•). Cette opération pourrait être représentée par un circuit électrique comportant des interrupteurs en série. Dans ce cas, il faut que tous les interrupteurs soient fermés en même temps pour que la lampe s’allume.
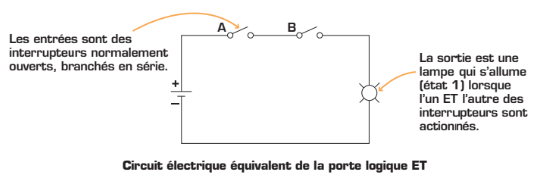
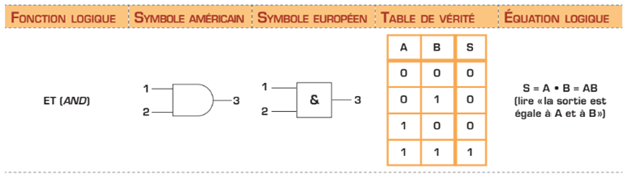
Le tableau qui suit montre le symbole de la porte logique qui effectue l’opération ET ainsi que la table de vérité et l’équation logique correspondantes. On peut remarquer, dans la table de vérité, que le signal de sortie est à « 1 » seulement lorsque tous les signaux d’entrée sont à « 1 ».
Porte logique NON
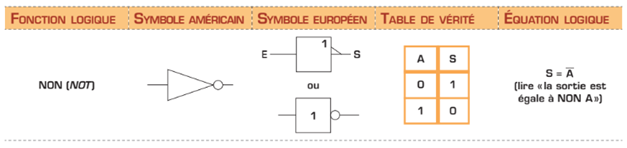
L’opérateur NON (en anglais, NOT) représente l’opération de négation, qui consiste à obtenir l’état inverse (complément) de celui de l’entrée. L’opérateur NON, communément appelé inverseur, ne s’applique qu’à une seule variable à la fois.

Porte logique OUI
L’opérateur OUI (en anglais, BUFFER) est utilisé presque exclusivement en électronique. Il ne modifie en rien l’état de l’entrée. Son rôle principal est d’amplifier le signal d’entrée pour qu’il soit utilisable. Il sert donc à régénérer un signal devenu trop faible.
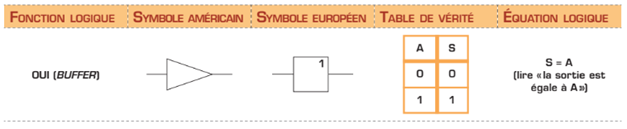
Quand on examine les caractéristiques de ces portes dans les manuels de fabricants (data book), on s’aperçoit que l’opérateur OUI possède des propriétés de sortie spécialement conçues pour attaquer des charges, soit une faible impédance de sortie et un courant maximal élevé. On peut donc le qualifier d’amplificateur de signal.
Portes logiques mixtes
On trouve également des portes logiques qui combinent les opérateurs vus précédemment. Elles sont en quelque sorte un mélange ou une variante de deux portes. C’est le cas des portes logiques: NON-OU, NON-ET, OU exclusif et NON-OU exclusif.
Portes logiques NON-OU et NON-ET
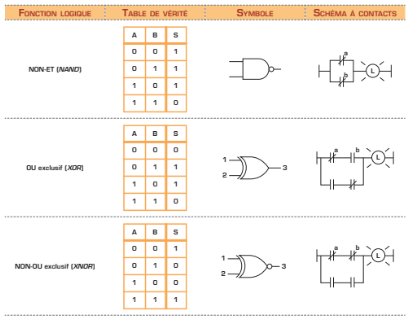
Les portes NON-OU et NON-ET (en anglais, NOR et NAND) sont tout simplement des portes OU et ET dont on a inversé la sortie.
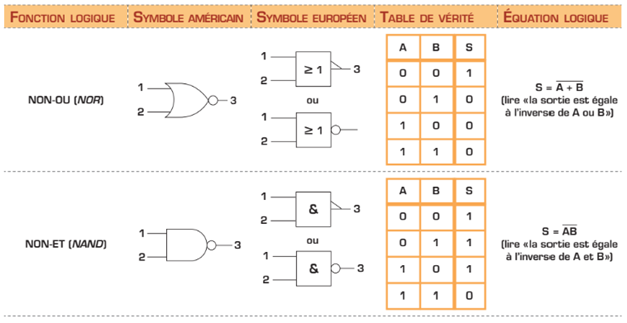
Portes logiques OU exclusif et NON-OU exclusif
Les portes OU exclusif et NON-OU (en anglais, XOR et XNOR) exclusif sont des comparateurs de signaux logiques. Dans le cas du OU exclusif, on obtient une valeur de «1» si une seule des entrées est à l’état logique «1». Cela signifie que si les deux entrées sont à «1», la sortie est à l’état «0»; l’inverse est aussi vrai.
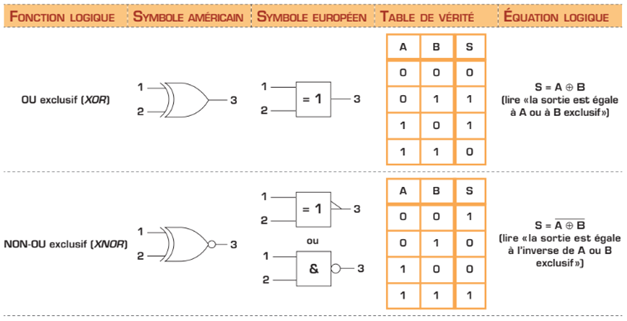
Ce type de portes peut être pratique pour détecter ou éviter les problèmes de fonctionnement d’un système. Par exemple, un ascenseur peut être en haut ou en bas, mais jamais à ces deux endroits en même temps. C’est ce type de situation qui nécessite l’utilisation de la fonction d’exclusivité. En ce qui a trait à l’écriture de l’équation, on désigne l’exclusivité par un cercle autour du «+» représentant le OU.
Circuits intégrés
La commande des systèmes industriels automatisés était autrefois possible grâce à la logique câblée (ou à relais) ou encore à la logique pneumatique ou hydraulique. L’utilisation des circuits intégrés a permis de remplacer, en partie, ces dispositifs volumineux par de plus petites pièces.
Les portes logiques, à partir desquelles sont construits les circuits logiques électroniques, sont disponibles sous la forme de circuits intégrés regroupant plusieurs portes en un seul composant. Ces circuits intégrés sont constitués d’un boîtier qui contient la puce, laquelle est reliée à l’extérieur par un certain nombre de pattes, généralement compris entre 14 et 28. La figure de la page suivante présente différents types de boîtiers de circuits intégrés, dont le plus répandu est le DIP (Dual In line Package).
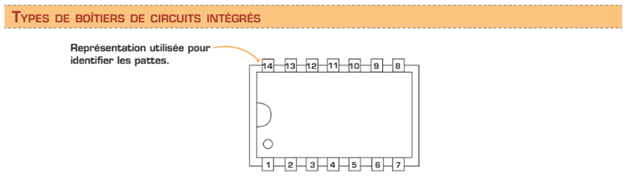
Notez que les pattes d’un C.I. peuvent être numérotées de plusieurs façons. Il est donc nécessaire de consulter la documentation du fabricant pour connaître la configuration du C.I. et l’ordre de numérotation des pattes. La figure ci-dessous montre un exemple de diagramme fonctionnel, celui d’un C.I. à trois portes NON-OU à trois entrées.
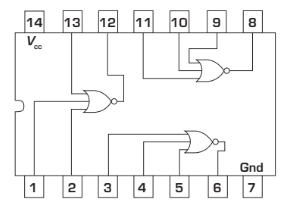
Technologies TTL et CMOS
Les circuits intégrés les plus employés relèvent de l’une ou l’autre des deux technologies suivantes: TTL (Transistor-Transistor Logic) et CMOS (Complementary Metal Oxide Semiconductor). Les circuits TTL sont construits avec des transistors bipolaires, alors que les CMOS emploient des transistors à effet de champ. Les circuits CMOS ont donc une très haute impédance d’entrée et consomment peu; par contre, ils sont plus fragiles.
Caractéristiques techniques des C.I.
Les caractéristiques importantes des C.I. concernent la tension d’alimentation, la consommation d’énergie, le temps de propagation ainsi que les tensions et les courants limites. Pour obtenir les caractéristiques d’un C.I. en particulier, vous n’avez qu’à consulter sa fiche technique. Le tableau suivant résume les principales caractéristiques des C.I. TTL et CMOS.
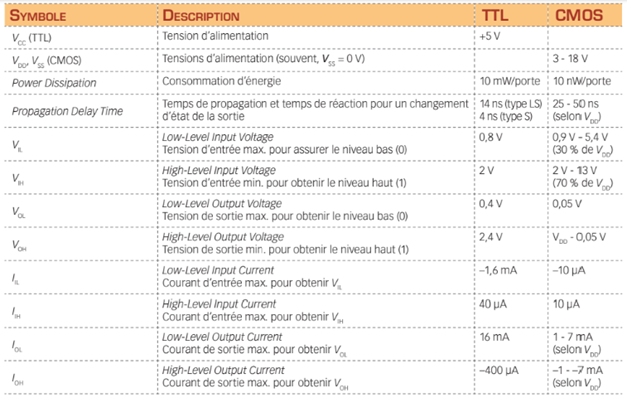
Zones d’immunité
D’après les caractéristiques de tension des C.I., on peut remarquer qu’il existe des plages de tension où l’état d’entrée ou de sortie est indéterminé. Ces plages, appelées zones d’immunité, servent essentiellement à éviter les fausses commutations (changements d’état) qui pourraient être causées par de petites variations de tension. Vous pouvez voir, dans la figure de la page suivante, les zones d’immunité à l’entrée et à la sortie des circuits TTL et CMOS.
Relais
Le relais est un composant qui agit un peu comme un interrupteur (ouvert/ fermé): il permet de commuter un circuit en fonction d’un signal. Il sert essentiellement à transmettre un signal d’un circuit de commande à un circuit de puissance, tout en assurant une isolation galvanique entre ces deux parties. Autrement dit, il n’y a aucune connexion physique entre la partie commande (alimentation de la bobine) et la partie puissance (les contacts du relais).
Structure d’un relais
Le relais est composé d’une bobine d’activation qui, lorsqu’elle est alimentée, transmet une force à un système de commutation à base de contacts. La tension appliquée sur la bobine produit un courant qui se manifeste par un champ magnétique autour de celle-ci. Le champ magnétique ainsi produit déplace une partie mobile (une lame montée sur un pivot, par exemple) qui ouvre ou ferme les contacts. Quand le courant cesse de circuler dans la bobine, les contacts reprennent leur position initiale grâce à un ressort de rappel.
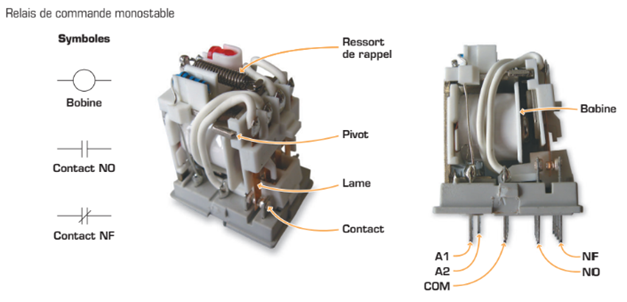
La figure montrant les deux projections d’un relais de commande monostable met en évidence ses principales parties. Ce relais polyvalent à quatre contacts constitue un choix idéal pour les commandes. Notez qu’il offre deux options de branchement: normalement ouvert (N.O.) ou normalement fermé (N.F.). Un contact N.O. est ouvert au repos (en position initiale), tandis qu’un contact N.F. est fermé dans la même condition.
Types de relais
Le choix d’un relais dépend de la nature de l’application. On en distingue généralement trois types: le relais de commande (control relay), le relais de puissance et le relais électronique. Le relais de puissance possède de plus gros contacts que le relais de commande ; ceux-ci peuvent donc supporter des courants plus intenses et interrompre des tensions plus élevées. Le contacteur appartient à la catégorie des relais de puissance puisque ses contacts supportent des courants supérieurs à 10 A. Le contacteur est utilisé pour couper le courant d’une charge inductive comme un moteur ou un transformateur.
Si le relais électronique sert aussi à commuter, il est conçu différemment des deux autres. Ses parties commande et puissance interagissent par couplage optique et non pas au moyen de pièces mobiles mues par une force magnétique, d’où son autre appellation de relais statique. De plus, sa sortie est le plus souvent un transistor ou un TRIAC. Il est également possible de distinguer les relais selon qu’ils sont monostable ou bistable. Le relais monostable est certainement le plus répandu en électricité industrielle. Ces caractéristiques typiques de fonctionnement sont les suivantes:
- Vitesse d’enclenchement: de 8 à 20 m/sec
- Nombre de cycles possibles: 100 millions
- Vitesse maximum: 15 commutations par seconde
Le relais bistable se caractérise par ses deux bobines montées en opposition. La mise sous tension d’une bobine déplace l’armature mobile. Les contacts restent en position active même lorsque la bobine n’est plus alimentée. Pour changer la position des contacts, il faut alimenter brièvement l’autre bobine. L’avantage de ce relais est qu’il n’a pas besoin d’un automaintien pour maintenir un signal actif. Par contre, il est désavantagé par son prix élevé. Notez que le relais bistable est moins répandu que le relais monostable en logique câblée.
Fonctions logiques à partir de relais
Le tableau qui suit permet d’établir un parallèle entre chaque symbole de porte logique et sa représentation à l’aide de relais, sous la forme d’un schéma à contacts ou diagramme échelle (ladder diagram). Chacune des fonctions logiques peut donc être matérialisée au moyen d’un ou de plusieurs relais.