NOTIONS MATHÉMATIQUES PRÉALABLES
La compréhension de l’électricité fait appel à des concepts abstraits. Bien qu’elle ne soit pas visible, l’électricité demeure prévisible, c’est-à-dire qu’en connaissant certaines données d’une installation nous pouvons déterminer, par des calculs, d’autres valeurs.
Priorité des opérations
Dans une expression mathématique, certaines étapes doivent être réalisées avant d’autres. C’est que qu’on appelle «l’ordre des opérations». Le tableau suivant résume l’ordre de priorité des fonctions mathématiques.


Isoler les variables
En électricité, vous aurez souvent à déterminer une grandeur (tension, courant, résistance, puissance, etc.) à partir de valeurs déjà données, la plupart du temps, par des instruments de mesure. Pour calculer une valeur manquante, vous devrez d’abord l’isoler dans la formule de base. L’isolement de variable consiste à séparer une variable (généralement exprimée par une lettre) prédéfinie du reste d’une expression mathématique pour qu’elle se trouve seule de son côté de l’expression.
Voici les trois principales règles à suivre pour isoler une variable :
- Il faut manipuler l’expression mathématique en appliquant la priorité des opérations vue précédemment.
- Lorsqu’un terme ou un bloc de termes est déplacé de l’autre côté de l’égalité, il faut faire l’opération mathématique contraire.
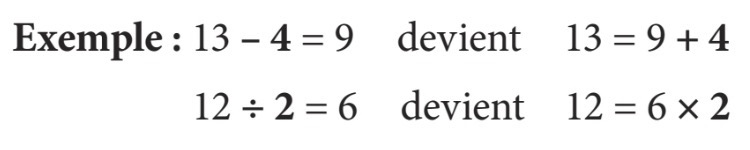
Notez que, si on déplace un terme entre parenthèses de l’autre côté de l’égalité, on effectuera l’opération mathématique contraire à celle qui est devant la parenthèse sans changer ce qui se trouve à l’intérieur de celle-ci.
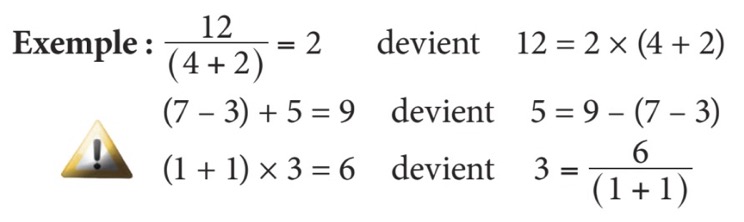
- Les opérations mathématiques ne peuvent être exécutées qu’avec les variables du même type et de même exposant.
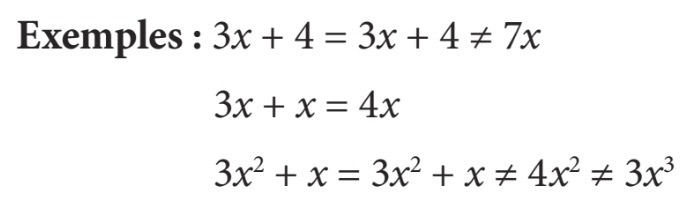
En résumé, pour isoler une variable, on se «débarrasse» des termes qui accompagnent la variable en les déplaçant de l’autre côté de l’équation. Ce processus se fait en plusieurs étapes. On commence par ce qui est le plus loin de la variable à isoler en le transférant de l’autre côté de l’égalité. Cela implique qu’on effectue l’opération mathématique contraire à ce qui se trouve dans la formule originale. On procède ainsi jusqu’à ce que la variable recherchée soit seule de son côté. S’il divise tout un côté de l’équation, considérez le dénominateur (diviseur) comme l’élément le plus éloigné de la variable : il doit donc être traité en premier.

Mise en évidence
Il arrive, à l’occasion, que l’on cherche à isoler une variable qui est multipliée (ou divisée) par différents facteurs à différents endroits dans une équation. Pour arriver à l’isoler, il faut obtenir un seul facteur qui affectera la variable à un seul endroit (ce facteur peut être le contenu d’une parenthèse). Le but sera donc de placer la variable à isoler devant une parenthèse et de déplacer ensuite cette parenthèse de l’autre côté.
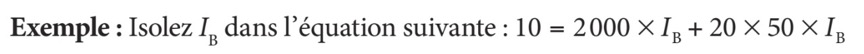
On peut d’abord récrire la formule en ajoutant des parenthèses pour bien illustrer que la multiplication a priorité sur l’addition.
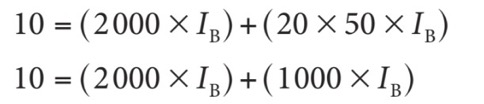
Le but, ici, c’est de récrire la même formule autrement en sortant la variable IB des parenthèses. Par contre, l’équation doit rester inchangée.
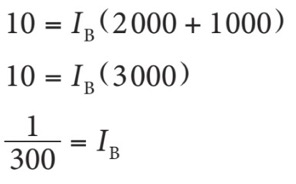
Voici un petit truc pour faire la mise en évidence : une fois les parenthèses formées, on inscrit, sur une nouvelle ligne, la variable à isoler, on ouvre la parenthèse puis on écrit les termes du premier groupe (on récrit tout ce qu’il y a sauf la variable qui est devant la parenthèse), on place ensuite le signe mathématique (par exemple, le signe de l’addition ou de la soustraction) qui unissait les deux parenthèses, puis on écrit les termes du second groupe, et on fait de même avec tous les termes.
Distributivité
La distributivité est le contraire de la mise en évidence. Elle sera utilisée lorsque la variable est additionnée (ou soustraite) à autre chose à l’intérieur de plusieurs parenthèses, elles-mêmes multipliées ou divisées par un facteur. Vous devez alors multiplier chaque terme (regroupement) contenu à l’intérieur de la parenthèse par le terme qui précède.
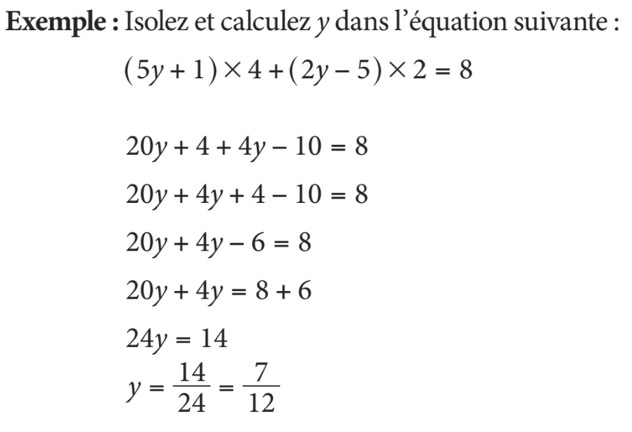
Loi des exposants
Lorsqu’on multiplie ou divise des nombres ou des variables possédant un exposant, on doit multiplier ou diviser les nombres ou variables tandis que les exposants seront additionnés ou soustraits, selon le cas.
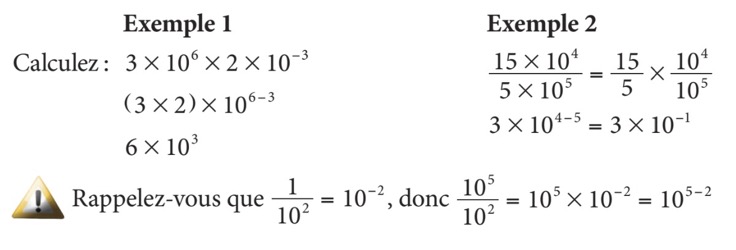
Théorème de Pythagore
Le théorème de Pythagore s’applique dans le cas d’un triangle rectangle, c’est-à-dire un triangle qui possède un angle droit. Cette formule est utile pour trouver la longueur d’un côté quand on connaît la longueur des deux autres côtés. Notez que le côté c s’appelle l’hypoténuse, qu’il est toujours opposé à l’angle droit et que c’est toujours le côté le plus long.
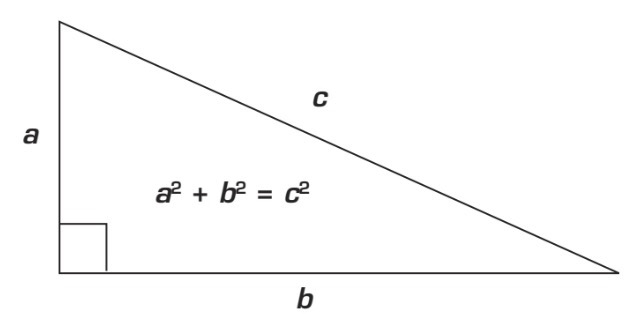
Pour trouver l’hypoténuse, additionnez les deux autres côtés au carré avant d’extraire la racine (addition, car c’est le côté le plus long). Par contre, si vous cherchez un côté différent de l’hypoténuse (a ou b ⇒ plus court), soustrayez de la longueur de l’hypoténuse au carré l’autre côté connu au carré avant d’extraire la racine (soustraction, car c’est un côté plus court).

Trigonométrie
Il arrive, à l’occasion, qu’on ait à trouver une longueur ou un angle, toujours dans le triangle vu précédemment. Pour ce faire, les trois fonctions trigonométriques sont fort utiles.

On peut se servir de ces fonctions pour trouver diverses mesures de longueur ou d’angle.

Pour vous souvenir du rapport (division) lié à la fonction, mémorisez le mot «indien» SOHCAHTOA.
SOH ⇒ Sinus = côté Opposé ÷ Hypoténuse
CAH ⇒ Cosinus = côté Adjacent ÷ Hypoténuse
TOA ⇒ Tangente = côté Opposé ÷ côté Adjacent

Préfixes
Les préfixes sont des petits mots qu’on utilise pour représenter une certaine quantité. Par exemple, kilomètre (km) représente 1 000 mètres et milligramme (mg) représente 1/1 000 de gramme.
Il existe plusieurs phénomènes physiques (électrique, pneumatique, hydraulique, mécanique, etc.) qu’on exprime par des mesures tantôt très grandes et tantôt très petites. Pour éviter d’inscrire des chiffres avec des tas de 0 consécutifs et pour diminuer les risques d’erreur, l’utilisation des préfixes s’impose. Le tableau ci-dessous présente les principaux préfixes avec lesquels vous aurez à travailler au cours de votre carrière. Certains vous sont déjà familiers, les autres ne tarderont pas à le devenir.

La plupart du temps, on inscrit des nombres entre 1 et 999 (et deux chiffres après la virgule) suivis du préfixe approprié.

L’utilisation appropriée de votre calculatrice fera toute la différence dans votre rapidité à traiter les préfixes. Il est très important que vous appreniez à l’utiliser correctement dès maintenant. Vous en serez récompensé tout au long de votre carrière. Il vous faut donc utiliser la touche 10x ou E ou EE ou EXP, selon le modèle que vous possédez. Notez bien qu’en utilisant ces touches vous ne devez pas entrer le nombre 10, car il est inclut dans la fonction. En règle générale, la calculatrice vous donne toujours la réponse en unités (au centre du tableau); c’est à vous à la reconvertir pour l’utiliser avec le préfixe approprié.
