COURANT ALTERNATIF
Bien qu’il ait été historiquement découvert après le courant continu, le courant alternatif (c.a.) est le plus répandu. En raison de son faible coût de production et de transport, et de sa facilité de distribution, il occupe une place majeure dans l’utilisation courante de l’électricité.
Pourquoi l’appelle-t-on «courant alternatif»? Comment le produit-on? Quelles sont ses caractéristiques? Avec quels appareils le mesure-t-on? Ce chapitre vous éclairera sur tous ces points, et plus encore. Vous y apprendrez d’abord les notions fondamentales de l’électromagnétisme associées au principe de production du courant alternatif par les alternateurs, puis vous vous familiariserez avec la terminologie et les valeurs qui caractérisent les ondes sinusoïdales produites. Enfin, vous aurez l’occasion de découvrir un nouvel appareil de mesure, l’oscilloscope. Bien qu’il s’agisse d’un outil principalement utilisé en électronique, et qu’il soit beaucoup plus encombrant que le multimètre, l’apprentissage de son utilisation est une étape essentielle de votre formation d’électricien. En effet, cet appareil vous permettra d’analyser et de mieux comprendre les ondes sinusoïdales qui caractérisent le courant alternatif.
Électricité et magnétisme
L’électricité et le magnétisme sont deux phénomènes physiques étroitement liés. On peut en effet produire l’un avec l’autre, et vice versa. Cette interaction entre l’électricité et le magnétisme, qu’on nomme «électromagnétisme», est un moyen très répandu de produire de l’électricité; c’est le moyen qu’on utilise, par exemple, dans une centrale hydroélectrique. Avant d’aborder l’électromagnétisme, voyons quelques notions sur le magnétisme et les phénomènes magnétiques associés aux aimants.
Notions de magnétisme
Comme vous l’avez déjà probablement constaté, les aimants ont la particularité d’attirer des particules de fer ou de se fixer sur des matériaux métalliques. Pensez, par exemple, aux aimants que vous utilisez peut- être pour fixer des notes sur un tableau magnétique ou sur la porte de votre réfrigérateur. Cette propriété d’attraction, qui est invisible, s’appelle magnétisme. Mais de quoi les aimants sont-ils constitués?
Aimants
Les aimants sont constitués de matériaux ferromagnétiques comme le fer, le cobalt et le nickel, ou d’alliages de ces métaux avec d’autres matériaux non ferromagnétiques tels que l’acier au silicium. On distingue généralement les aimants naturels et les aimants artificiels. Les aimants naturels contiennent de la magnétite, un minerai de fer noirâtre dont les propriétés magnétiques sont connues depuis l’Antiquité. Les aimants artificiels sont des morceaux d’acier qui ont subi un traitement spécial pour devenir aimantés. De nos jours, on utilise les aimants dans de nombreuses applications industrielles et électroniques, comme les moteurs, les alternateurs et les haut-parleurs, et dans certains appareils de mesure.
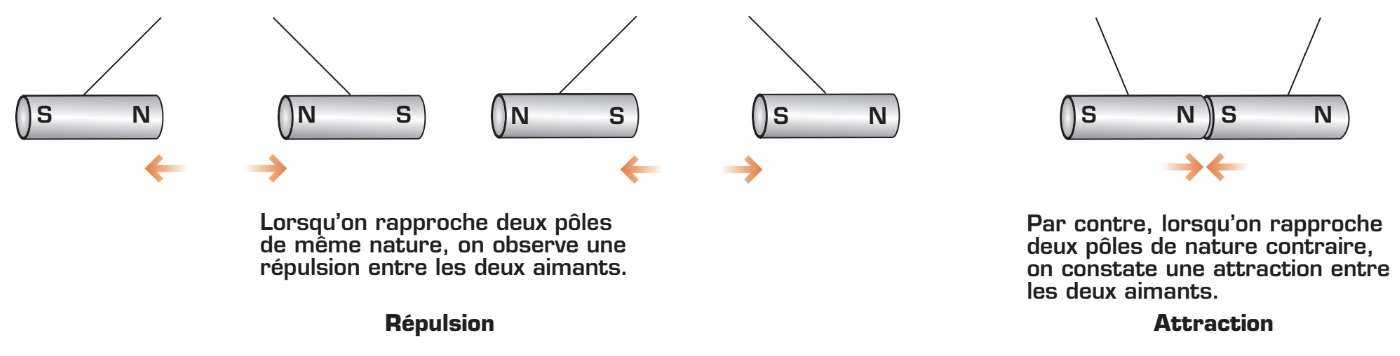
Pôles magnétiques des aimants
Tous les aimants possèdent deux pôles magnétiques qui sont situés à leurs extrémités : on les appelle pôle nord et pôle sud. Par convention, le pôle nord d’un aimant est l’extrémité qui s’oriente vers le pôle Nord géographique de la Terre, tandis que son pôle sud pointe vers le pôle Sud terrestre. Par exemple, quand vous utilisez une boussole pour vous repérer, l’extrémité de l’aiguille aimantée qui pointe toujours vers le pôle Nord géographique représente le pôle nord de l’aimant. Notez que, si vous coupez un aimant en deux, vous aurez entre les mains deux nouveaux aimants ayant chacun un pôle nord et un pôle sud. Comme vous l’avez peut-être déjà observé, les pôles de même nature se repoussent tandis que les pôles de natures contraires s’attirent. C’est ce qu’on appelle la «loi des pôles magnétiques».
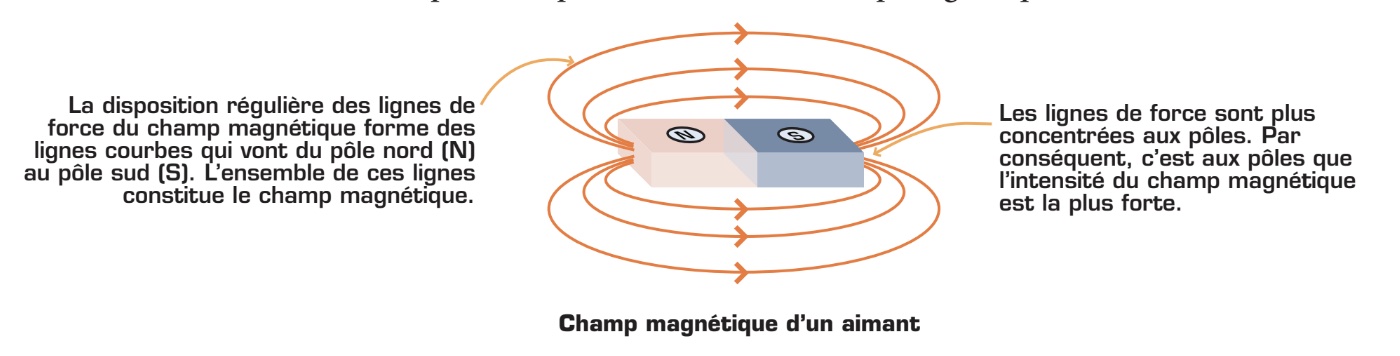
Champ magnétique
En exerçant une force magnétique invisible, un aimant modifie les propriétés magnétiques de l’espace qui l’entoure. Le champ magnétique représente ainsi l’influence magnétique de l’aimant dans l’espace. Pour représenter un champ magnétique autour d’un aimant, on a recours au concept des lignes de force, appelées aussi «lignes de champ» ou «lignes de flux». La figure ci-dessous montre l’aspect que prennent les lignes de force autour d’un aimant linéaire. Par convention, on a établi que ces lignes invisibles sortent par le pôle nord pour entrer par le pôle sud. Dans les faits, elles circulent autour et à l’intérieur de l’aimant, formant ainsi des boucles fermées. Plus on s’éloigne des pôles, plus les lignes deviennent espacées et plus l’intensité du champ magnétique diminue.
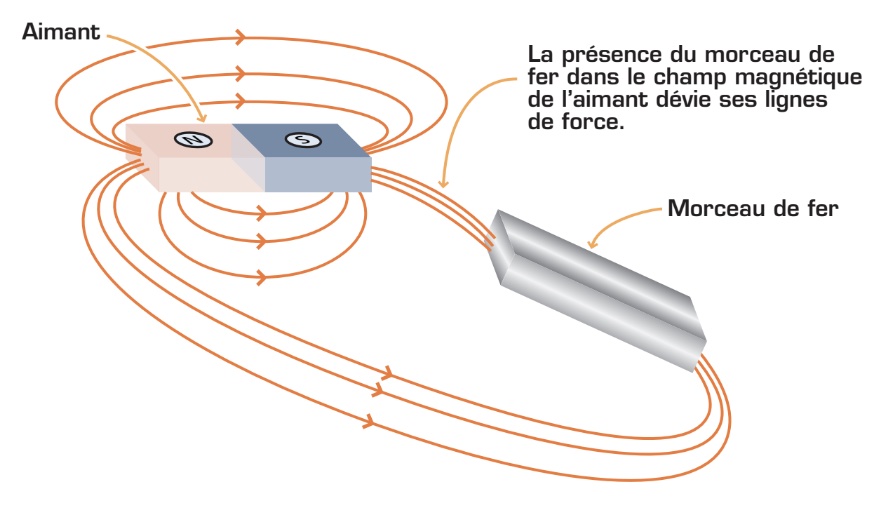
Effet du fer sur le champ magnétique
Voyons maintenant l’effet du fer sur le champ magnétique. Si on introduit un morceau de fer doux dans un champ magnétique, les lignes de force de l’aimant se déforment pour se concentrer sur le fer. Ce phénomène résulte du fait que le fer est beaucoup plus «perméable» aux lignes de force magnétiques que l’air. Cet effet du fer est mis à profit, entre autres, dans les câbles blindés qui sont utilisés pour la transmission de signaux électriques afin de les protéger contre les influences d’un champ magnétique extérieur. C’est aussi cet effet qui est utilisé dans les transformateurs.
Électromagnétisme
L’électromagnétisme est l’étude des interactions entre le champ magnétique et le courant électrique. Il regroupe à la fois les effets magnétiques qui sont engendrés par la circulation d’un courant électrique dans un conducteur et les effets du champ magnétique sur un courant qui circule dans un conducteur.
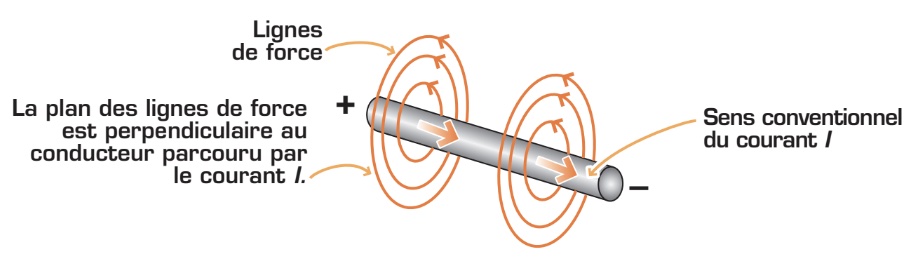
Effet magnétique du courant électrique
Comme nous l’avons déjà mentionné à quelques reprises dans les premiers chapitres de ce guide, lorsqu’un courant électrique circule dans un conducteur, il se crée un champ magnétique autour de ce conducteur. Ce champ magnétique possède les cinq caractéristiques suivantes :
-
il se trouve dans un plan perpendiculaire au courant qui le produit;
-
ses lignes de force sont symétriques par rapport au centre du conducteur;
-
il agit sur toute la longueur du conducteur;
-
son intensité diminue à mesure que l’on s’éloigne du conducteur;
-
il disparaît dès que le courant cesse de circuler dans le conducteur.
La figure ci-dessous montre un champ magnétique autour d’un conducteur parcouru par un courant électrique.
Solénoïde
Un solénoïde est une bobine constituée de plusieurs tours (appelés « spires») de fil conducteur. La circulation d’un courant dans chacune des spires de fil produit un champ magnétique comparable à celui d’un aimant linéaire, laissant aux extrémités de la bobine un pôle nord et un pôle sud. Comme le montre la figure ci-dessous, une autre règle de la main droite permet de déterminer la polarité magnétique de la bobine.
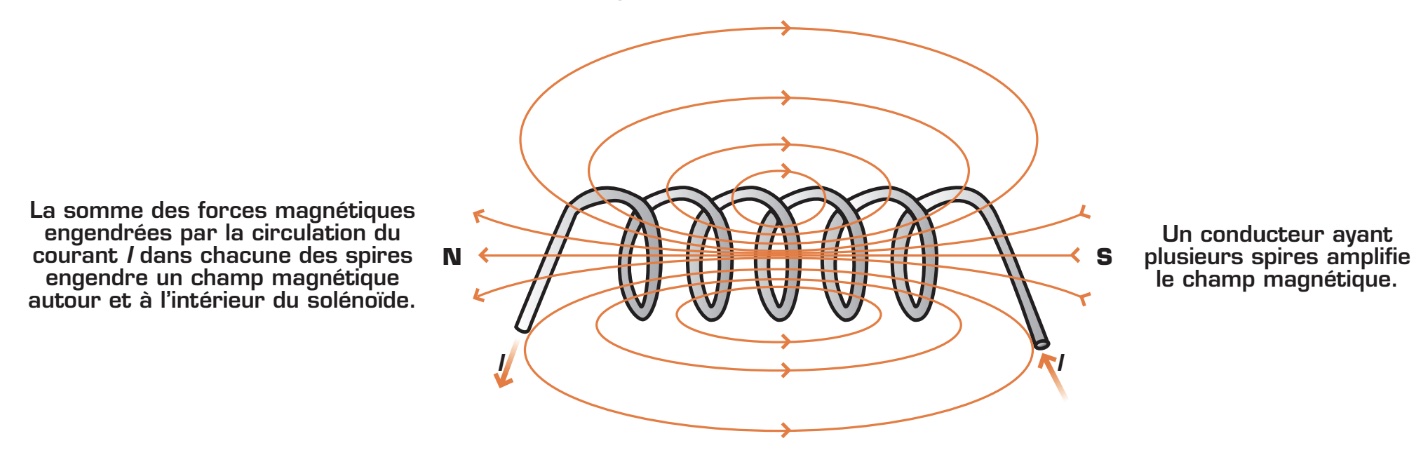
Pour augmenter l’intensité du champ magnétique, on monte la bobine de fil autour d’un noyau ferromagnétique (généralement du fer doux). Le dispositif qui en résulte s’appelle un électroaimant. La force électromagnétique détermine la puissance d’un électroaimant. Elle dépend de l’intensité du courant circulant dans la bobine, du nombre de tours de fil et de la nature du noyau ferromagnétique. Les électroaimants sont fréquemment utilisés dans plusieurs applications, comme les moteurs, les relais électromagnétiques et les sonnettes électriques. On les utilise, par exemple, pour créer un champ magnétique intense qui sert à générer des tensions électriques ou à produire un couple moteur.
Induction électromagnétique
L’induction électromagnétique résulte des interactions entre les conducteurs, les courants électriques et les champs magnétiques. Elle se manifeste principalement de trois façons. Examinons rapidement chacune d’elles :
-
Lorsqu’on place un conducteur porteur de courant dans un champ magnétique, le conducteur tend à se déplacer. C’est en quelque sorte l’action motrice de l’induction électromagnétique. Ce phénomène est à la base du fonctionnement des moteurs électriques.
-
Lorsqu’on place un conducteur non alimenté dans un champ magnétique variable, une tension est induite (fabriquée) dans le conducteur. Supposons que deux bobines de fil se trouvent à proximité l’une de l’autre et que l’une est alimentée. Les variations du champ magnétique produit par la bobine alimentée induisent une tension dans une seconde bobine (voir figure à la page suivante). Cet effet inductif d’une bobine sur une autre s’appelle l’«inductance mutuelle». Il est exploité dans les transformateurs.
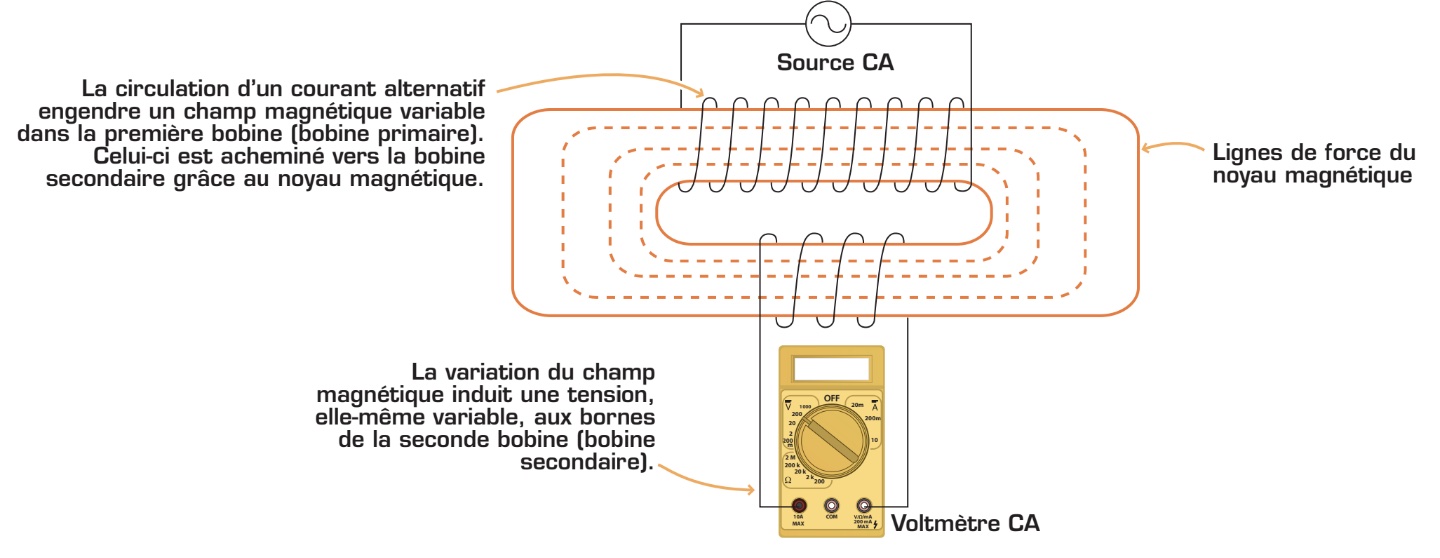
- Enfin, lorsqu’on déplace un conducteur non alimenté dans un champ magnétique, on induit une tension à ses extrémités, appelée aussi force électromotrice (f. é. m.). C’est l’action génératrice de l’induction électromagnétique. La valeur de la tension induite dépend à la fois de l’intensité du champ magnétique, du sens du déplacement du conducteur dans le champ magnétique, de la longueur du conducteur et de la vitesse de déplacement du conducteur. Le fonctionnement des alternateurs est basé sur le mouvement d’un cadre mobile dans un champ magnétique.
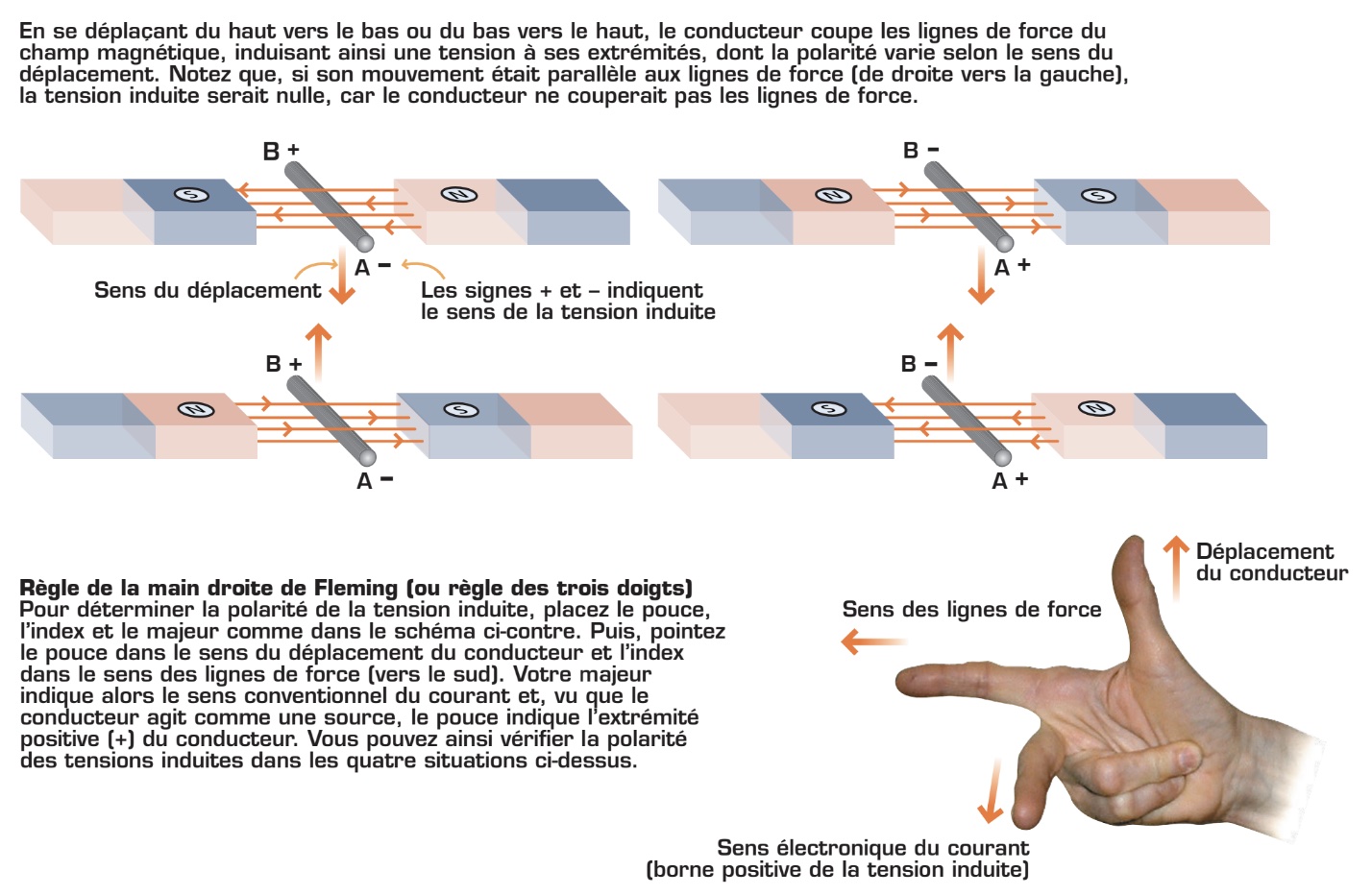
Production d’une onde sinusoïdale
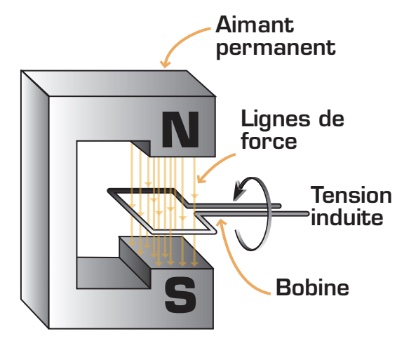
Maintenant que vous avez acquis les bases de l’électromagnétisme, voyons comment produire un courant alternatif. L’alternateur est un appareil qui produit un courant électrique alternatif de forme sinusoïdale. Son principe de fonctionnement repose sur l’induction électromagnétique.
Alternateur élémentaire
La figure ci-dessous présente un alternateur élémentaire. Il est constitué d’un aimant permanent qui produit le champ magnétique et d’un conducteur mobile, sous la forme d’un cadre, nommé «bobine » ou «enroulement». La bobine est entraînée par une force mécanique externe qui lui procure un mouvement de rotation à l’intérieur même du champ magnétique. Cette situation induit dans la bobine une tension (ou f. é. m.) qu’il est possible de mesurer à ses extrémités.
Dans un alternateur, la bobine tourne à une vitesse constante, formant ainsi un mouvement périodique. Comme le mouvement de la bobine est périodique, la tension induite l’est également. Cependant, la valeur de la tension induite n’est pas constante puisque la quantité de lignes de force croisées varie en fonction du temps (selon la position du cadre). Cette valeur dépend donc de l’angle formé par le déplacement de la bobine et les lignes de force du champ magnétique, tel qu’il est illustré dans la figure. À l’instant où le déplacement de la bobine est perpendiculaire aux lignes de force (positions 90° et 270°), la tension induite est maximale. Par contre, lorsque le déplacement de la bobine est parallèle aux lignes de force (positions 0° et 180°), la tension induite est nulle. Par ailleurs, la polarité de la tension induite change (alterne) à chaque demi-rotation, d’où le nom de «tension alternative». Cela est dû au fait que chaque pôle de l’aimant génère sa propre polarité de tension. Ainsi, la demi-rotation de 0° à 180° de la bobine induit une tension positive (alternance positive), alors que la demi-rotation de 180° à 360° induit une tension négative (alternance négative). La figure ci-dessous montre le cycle de la tension induite ; il correspond à un tour complet de la bobine dans son champ magnétique (de 0° à 360°). Lorsque l’on représente graphiquement les différentes valeurs que prend la tension au cours du temps, on obtient ainsi une onde de forme sinusoïdale.
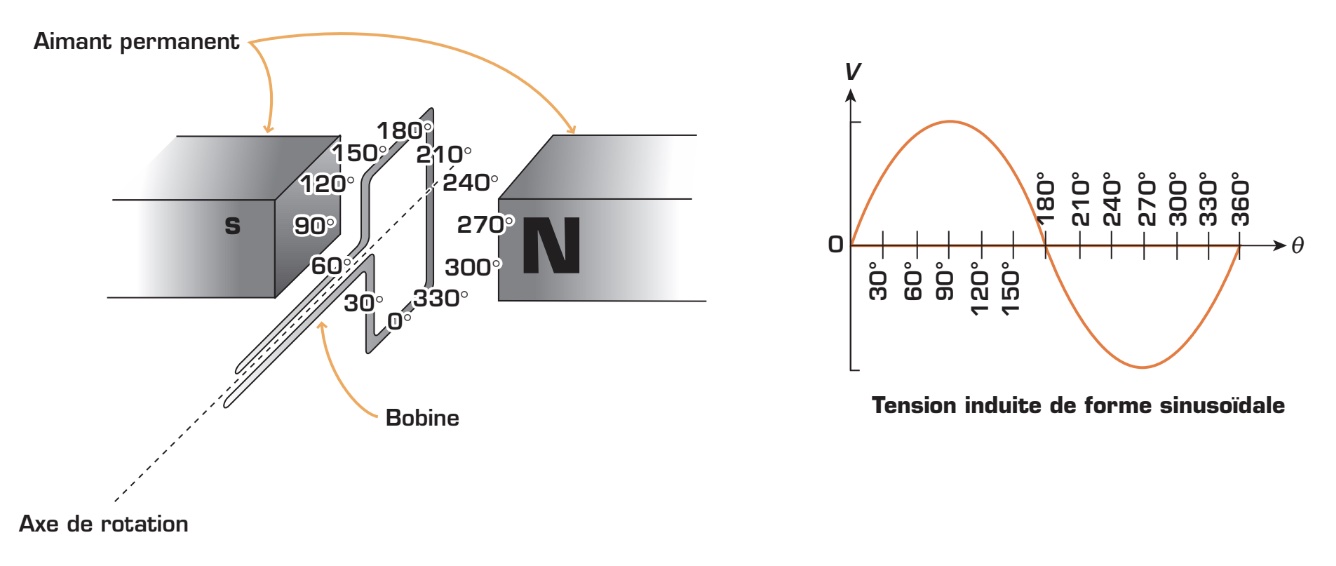
- En un tour complet (cycle), la bobine induit une tension de forme sinusoïdale. Celle-ci atteint sa valeur maximale aux positions 90° et 270° lorsque le déplacement de la bobine est perpendiculaire aux lignes de force du champ magnétique induit par l’aimant. Elle est nulle aux positions 0°, 180° et 360°, car le déplacement de la bobine est alors parallèle aux lignes de force.
- La polarité de la tension change à chaque demi-cycle, produisant ainsi une inversion du sens du courant dans le conducteur mobile (bobine).
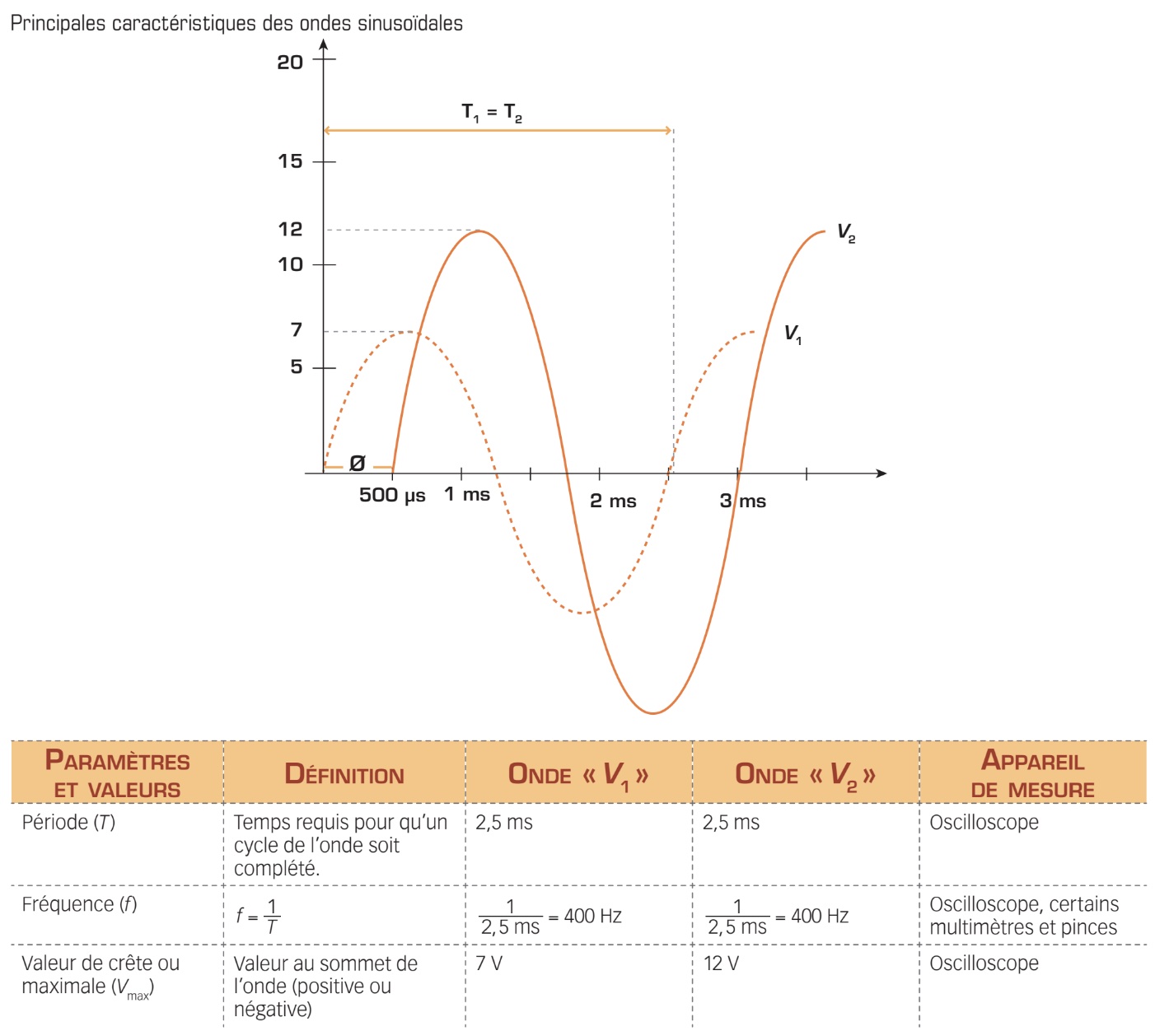
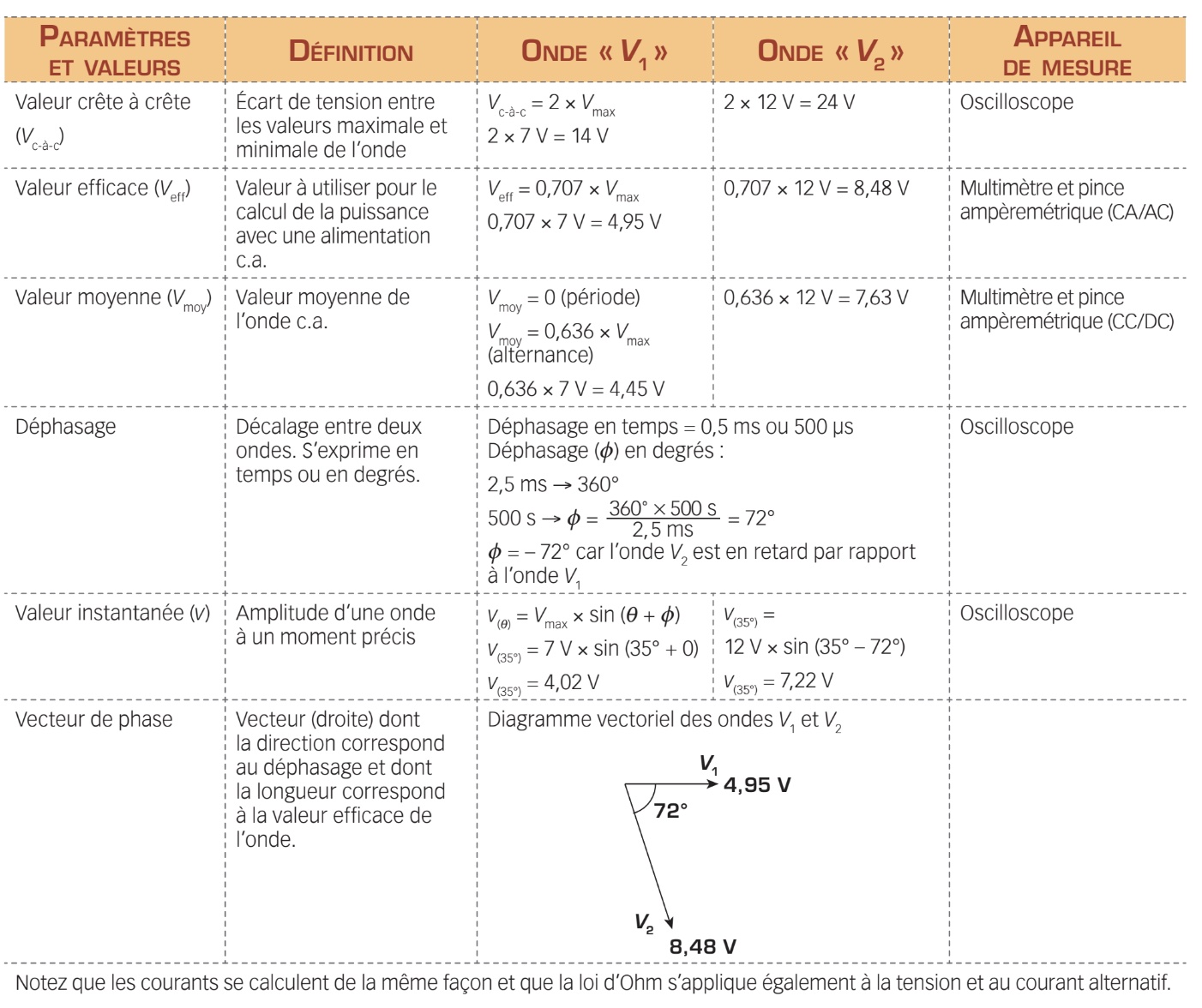
Termes relatifs à l’onde sinusoïdale
L’onde sinusoïdale est une représentation graphique des variations de la tension alternative ou du courant alternatif au cours du temps. Elle possède plusieurs caractéristiques, chacune d’elles portant un nom particulier. Certaines sont liées, d’autres, non. C’est ce que nous allons découvrir.
Période
La période est le temps que prend l’onde pour compléter un cycle (alternance positive et négative). Attention : pour déterminer ce temps, il n’est pas impératif de considérer l’origine. L’important est de partir d’un certain point de tension ou de courant (axe vertical des y) et de calculer le temps nécessaire (axe horizontal des x) pour revenir au même point dans le cycle suivant. Symbolisée par T, la période est habituellement exprimée en secondes (s).
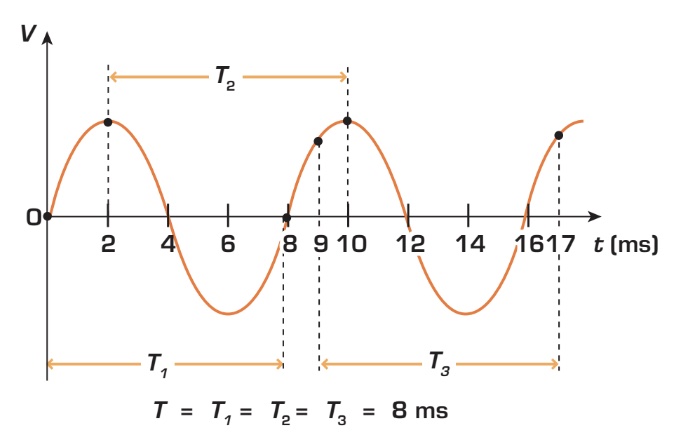
Fréquence
Communément, la fréquence est le nombre de répétitions par unité de temps. Par exemple, à quelle fréquence vous entraînez-vous? Réponse : trois fois par semaine ou… trois fois par mois. En électricité, la fréquence d’une onde sinusoïdale est le nombre de cycles effectués en une seconde. Symbolisée par la lettre f , on l’exprime en hertz (Hz). Il existe un lien entre la période et la fréquence. En effet, la fréquence est inversement proportionnelle à la période :
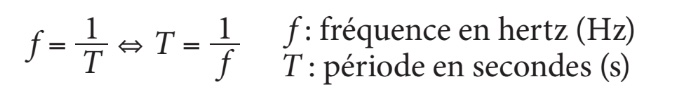
Alternance
Dans un cycle ou une période de l’onde sinusoïdale, il y a deux alternances : une alternance positive et une alternance négative.
L’alternance positive est la partie de l’onde sinusoïdale située au-dessus de l’axe horizontal des x (l’axe de temps). Elle correspond à une tension positive (ou à un courant positif). Par contre, une tension négative (ou un courant négatif) est représentée par l’alternance négative, qui se trouve sous l’axe horizontal.
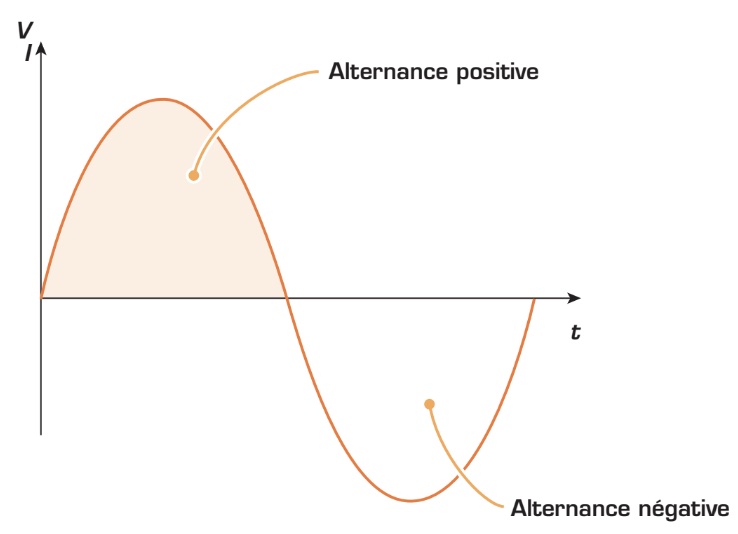
Amplitude
Souvent associée à la valeur maximale d’une onde, l’amplitude est, par définition, la valeur d’une onde à un moment précis dans le temps. Contrairement au courant continu, l’amplitude de l’onde sinusoïdale varie en fonction du temps. La figure ci-dessous montre un exemple de l’amplitude d’une onde sinusoïdale à différents points.
Valeurs de l’onde sinusoïdale
Vous savez maintenant que la valeur de la tension ou du courant alternatif varie en fonction du temps, suivant une courbe de forme sinusoïdale. Cette onde sinusoïdale présente plusieurs valeurs caractéristiques que vous devez connaître.
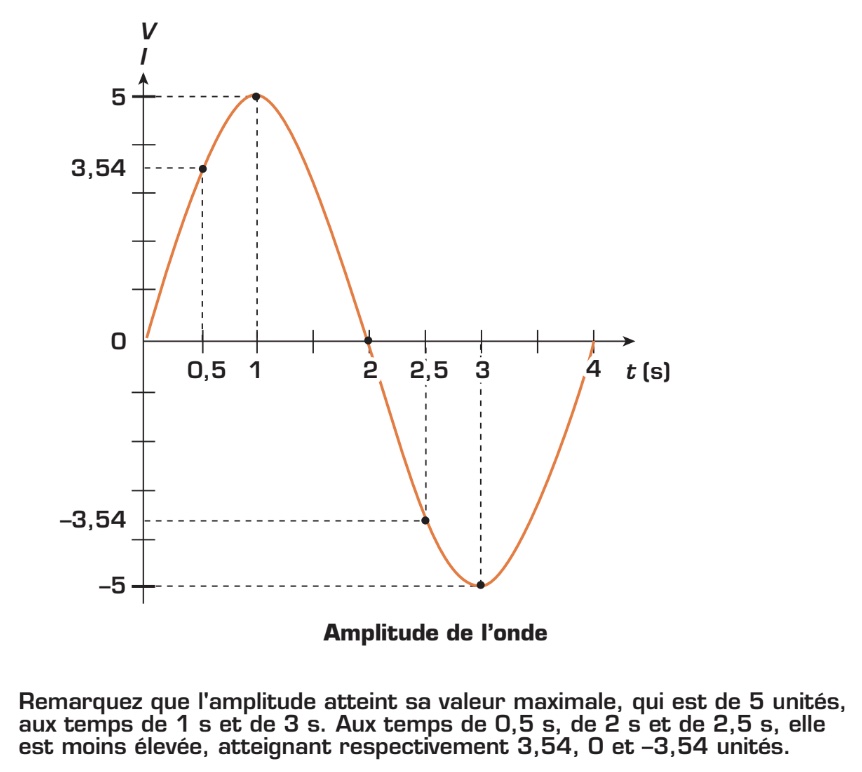
Valeur de crête
La valeur de crête, aussi appelée valeur maximale, correspond à la plus grande valeur (positive ou négative) que peut prendre l’onde sinusoïdale. S’il s’agit d’une tension alternative, on la représente par les symboles Vm, Vmax ou VP. Les symboles Im, Imax ou IP sont utilisés pour désigner la valeur maximale d’un courant alternatif. Notez que l’indice p provient du terme anglais peak, qui signifie «crête»
Observez ci-dessous une courbe de tension et ses deux valeurs de crête de même amplitude mais de polarités inverses. On parle alors de crête positive et de crête négative.

La valeur de crête est la référence qui permet de déterminer toutes les autres valeurs relatives à l’onde sinusoïdale. Sachez dès à présent que la tension de crête d’une onde sinusoïdale peut être mesurée par un instrument de mesure qu’on appelle oscilloscope.
Valeur crête à crête La valeur crête à crête est définie par la distance entre la crête positive et la crête négative. Dans le cas d’une tension alternative, on la représente par les symboles Vc-à-c ou V p-p ; s’il s’agit d’un courant alternatif, on utilise les symboles Ic-à-c ou I p-p. Notez que l’indice p-p vient de l’expression anglaise peak-to-peak.
Étant donné que les deux crêtes d’une onde sinusoïdale ont la même grandeur, il est permis de dire que la valeur de crête à crête est égale à deux fois la valeur maximale de l’onde.
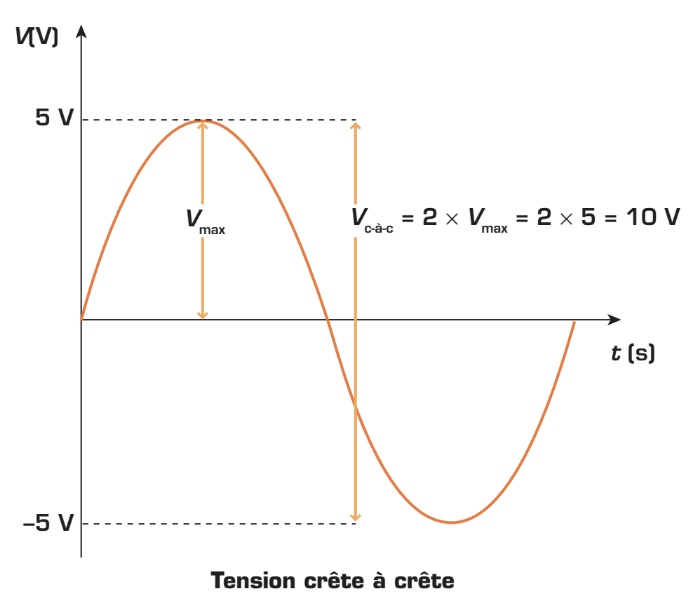
Dans la figure ci-dessus, la valeur crête à crête de l’onde est de 10 V. Encore une fois, cette valeur peut être mesurée directement à l’oscilloscope.
Valeur moyenne
La valeur moyenne d’une onde correspond à la somme de toutes les valeurs instantanées de l’onde divisée par le temps (période). Elle est représentée par les symboles V moy ou Vcc (pour une tension) ou I moy ou Icc (pour un courant).
La valeur moyenne d’une onde sinusoïdale d’un cycle ou d’une période est nulle, car la somme de toutes les valeurs instantanées positives est annulée par la somme de toutes les valeurs instantanées négatives. Par contre, la valeur moyenne d’une demi-alternance (demi-cycle) correspond à 63,6 % de la valeur maximale de l’onde sinusoïdale. On l’obtient par les formules suivantes :
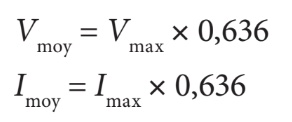
La valeur moyenne d’une onde alternative peut être mesurée à l’aide du multimètre sur l’échelle de tension ou courant continu (échelle c.c.), d’où l’utilisation des symboles Vcc et Icc.
Valeur efficace
Parmi les différentes valeurs caractéristiques de l’onde sinusoïdale, la valeur efficace est la plus importante. Comme vous venez de le voir, la valeur d’une tension ou d’un courant alternatif varie continuellement en fonction du temps, de sorte que sa moyenne sur un cycle est nulle. Cependant, la tension ou le courant alternatif fournit toujours une puissance non nulle à la charge, et ce, peu importe la variation de valeur et de polarité. De ce constat découle la notion de valeur efficace de la tension ou du courant. On l’utilise donc pour déterminer la puissance que produit une tension ou un courant alternatif à une charge.
La valeur efficace d’une tension (Veff) ou d’un courant (Ieff) sinusoïdal est égale à la valeur équivalente d’un courant continu qui produit la même puissance. Donc, si on applique ce principe à un circuit simple composé d’une source de tension c.a. et d’une résistance, la valeur efficace d’une onde sinusoïdale est égale à la tension continue qui dégage la même quantité de chaleur (puissance) dans cette même résistance. Voyons dans l’exemple suivant une illustration de ce principe.

Par définition, la valeur efficace d’une onde sinusoïdale correspond à 70,7 % de la valeur maximale de l’onde.

Notez que ce sont ces valeurs efficaces qui sont données par le multimètre lorsqu’il mesure une tension ou un courant alternatif (échelle c.a.). Les symboles Vca et Ica représentent donc respectivement la valeur efficace de la tension et celle du courant d’une onde sinusoïdale. Dans la très grande majorité des cas, les indications concernant les tensions et les courants alternatifs sont données en valeur efficace, car c’est à l’aide de cette valeur que l’on peut calculer les puissances du circuit.
Souvenez-vous bien que la valeur efficace d’un signal alternatif (Veff ou Ieff) correspond à la valeur équivalente d’une tension ou d’un courant continu qui produit la même puissance. Notez qu’elle peut aussi être représentée par les symboles VRMS ou IRMS. L’abréviation «RMS» vient de l’expression anglaise root-mean-square. Sachez aussi que, lorsqu’une tension ou un courant alternatif est inscrit sans indice, il s’agit d’une valeur efficace. Les appareils de mesure à l’échelle c.a. (CA/AC) indiquent la valeur efficace de l’onde.
Courant de l’onde sinusoïdale
Lorsqu’un circuit est alimenté par une source à courant alternatif, la loi d’Ohm reste valable et peut être employée de la même manière qu’on l’utilise lorsqu’on travaille sur des circuits à courant continu. En plus de résumer l’ensemble des caractéristiques d’une onde sinusoïdale, l’exemple qui suit montre comment appliquer la loi d’Ohm à un circuit c.a.


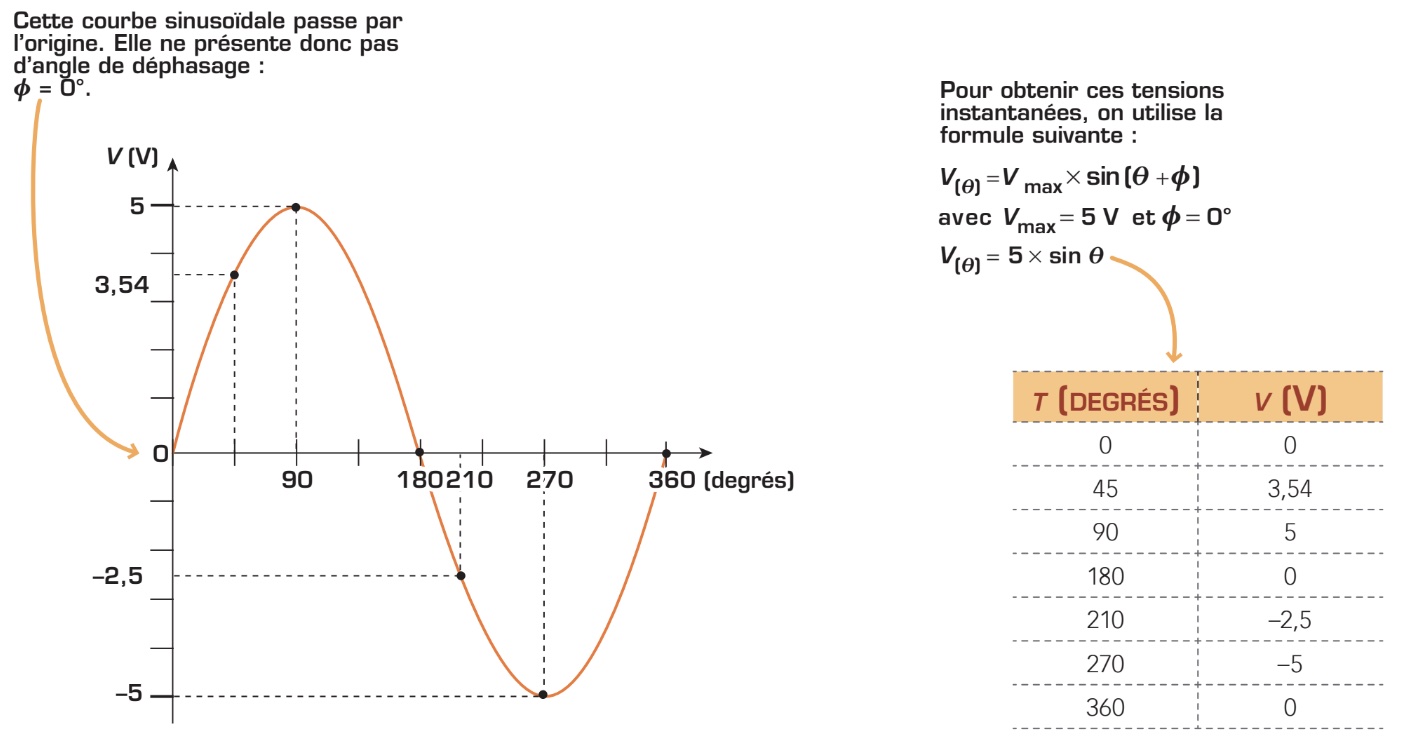
Valeur instantanée
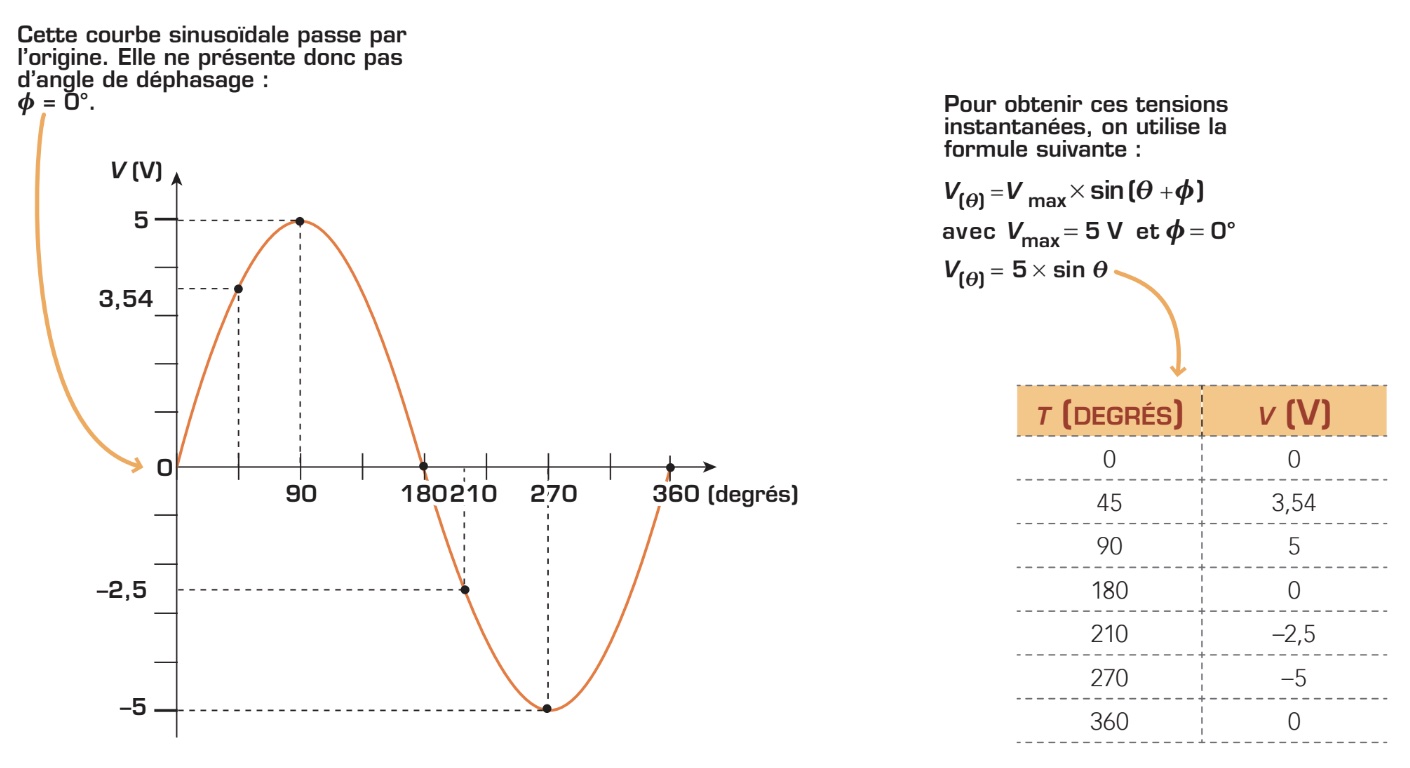
La valeur instantanée représente la valeur réelle de la tension ou du courant alternatif à un moment précis. Comme nous l’avons vu précédemment, c’est, en quelque sorte, une autre façon de nommer l’amplitude. Pour calculer la valeur instantanée d’une onde sinusoïdale, on doit appliquer les formules suivantes :

Cette formule vous sera surtout utile dans le module 13, qui est consacré aux circuits électroniques, particulièrement lorsqu’il sera question de l’amorçage des thyristors.
Observez ci-dessous différentes valeurs instantanées d’une tension alternative qui sont calculées à l’aide de la formule précédente.
Relations de phase
Pour bien comprendre ce qu’est une relation de phase, imaginez la situation suivante. L’entreprise ELICE a divisé son personnel en deux groupes de travail. Le groupe A s’occupe de la production et travaille de 8 h à 16 h. Le groupe B, quant à lui, est chargé de l’emballage et travaille de 10 h à 18 h. Même si tout le personnel travaille 8 heures par jour (les employés ont tous la même période), il existe un décalage de deux heures entre l’horaire de travail du premier groupe et celui du second.
De la même manière, il peut également exister, entre deux ondes sinusoïdales, une relation de phase marquée par un décalage.
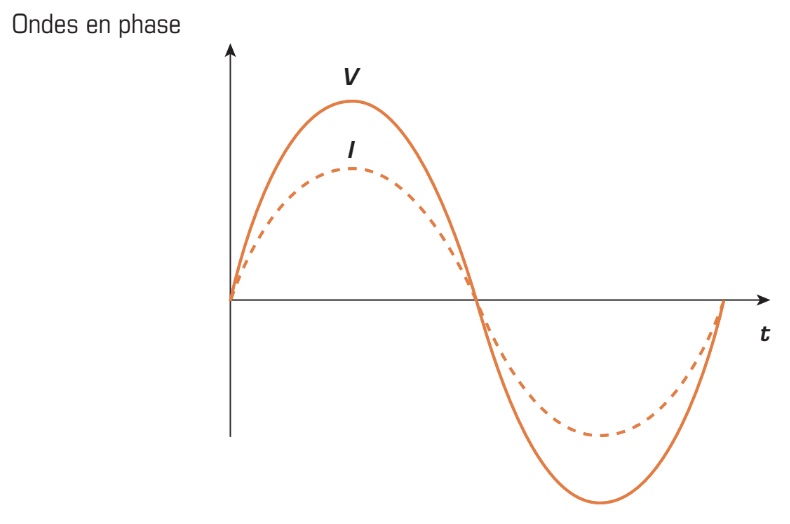
Ondes en phase
Si tout le personnel de l’entreprise ELICE commençait et terminait son quart de travail aux mêmes heures, on pourrait affirmer que tous les employés de cette entreprise sont en phase. Cela signifierait qu’il n’y a aucun décalage entre les horaires de travail. Dans les circuits électriques, il y a toujours un minimum de deux signaux qui circulent simultanément, soit la tension et le courant.
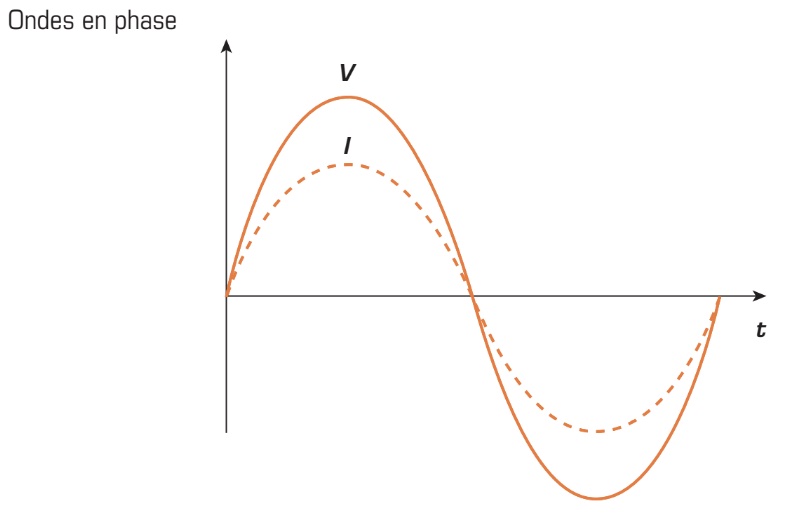
Dans les circuits résistifs, ces deux signaux sont en phase. Cela signifie qu’ils débutent en même temps et suivent le même parcours sans nécessairement avoir la même amplitude (deux ondes en phase).
Déphasage
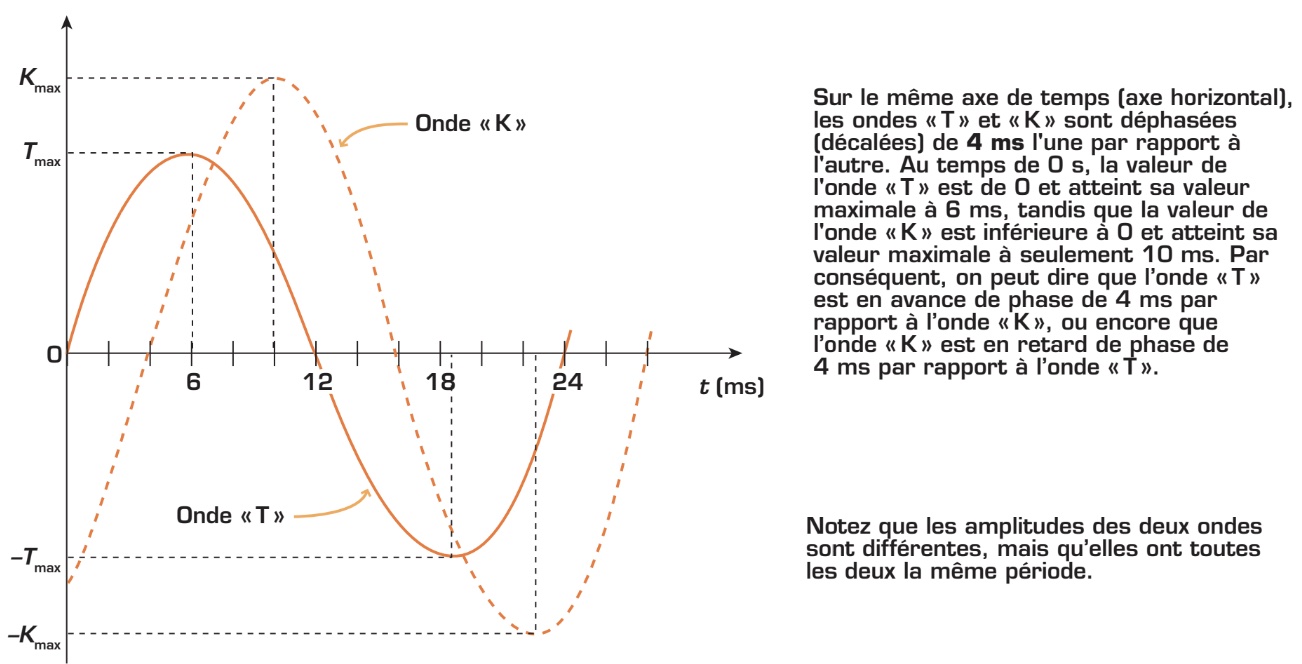
Le déphasage représente le décalage de temps (ou de degré) entre deux ondes. Le déphasage ne peut être défini qu’en fonction de deux ondes de même période (ou de même fréquence) et uniquement en fonction d’une onde par rapport à une autre (on a donc besoin d’une onde de référence). Observez ci-après le déphasage entre les ondes «T» et «K».
Le déphasage est le terme général utilisé pour désigner le décalage entre deux ondes. Cependant, l’utilisation des expressions «avance de phase» et «retard de phase» permet de préciser la relation de phase entre deux signaux. Notez que la relation de phase peut exister entre deux tensions ou deux courants, ou entre une tension et un courant.
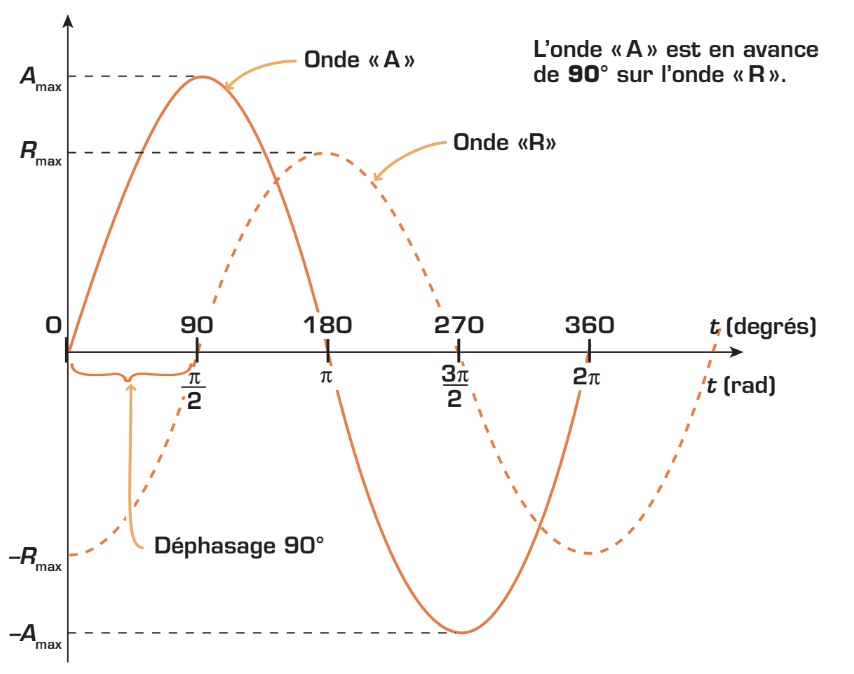
Angle de phase
Lorsque la bobine de l’alternateur fait un tour complet dans le champ magnétique, un cycle de tension de forme sinusoïdale est produit. Ce cycle correspond toujours à 360° (ou 2π radians). Ainsi, le déphasage entre deux ondes peut non seulement être exprimé en temps, comme dans l'exemple précédent, mais aussi en degrés (ou en radians). Lorsque le déphasage est exprimé en degrés (ou en radians), il est appelé « angle de phase ». Observez ci-dessous un angle de phase de 90° entre deux ondes.

Observez ci-dessous différentes valeurs instantanées d’une tension alternative qui sont calculées à l’aide de la formule précédente.
Relations de phase
Pour bien comprendre ce qu’est une relation de phase, imaginez la situation suivante. L’entreprise ELICE a divisé son personnel en deux groupes de travail. Le groupe A s’occupe de la production et travaille de 8 h à 16 h. Le groupe B, quant à lui, est chargé de l’emballage et travaille de 10 h à 18 h. Même si tout le personnel travaille 8 heures par jour (les employés ont tous la même période), il existe un décalage de deux heures entre l’horaire de travail du premier groupe et celui du second.
De la même manière, il peut également exister, entre deux ondes sinusoïdales, une relation de phase marquée par un décalage
Ondes en phase
Si tout le personnel de l’entreprise ELICE commençait et terminait son quart de travail aux mêmes heures, on pourrait affirmer que tous les employés de cette entreprise sont en phase. Cela signifierait qu’il n’y a aucun décalage entre les horaires de travail.
Dans les circuits électriques, il y a toujours un minimum de deux signaux qui circulent simultanément, soit la tension et le courant. Dans les circuits résistifs, ces deux signaux sont en phase. Cela signifie qu’ils débutent en même temps et suivent le même parcours sans nécessairement avoir la même amplitude (deux ondes en phase).
Déphasage
Le déphasage représente le décalage de temps (ou de degré) entre deux ondes. Le déphasage ne peut être défini qu’en fonction de deux ondes de même période (ou de même fréquence) et uniquement en fonction d’une onde par rapport à une autre (on a donc besoin d’une onde de référence). Observez ci-après le déphasage entre les ondes «T» et «K».
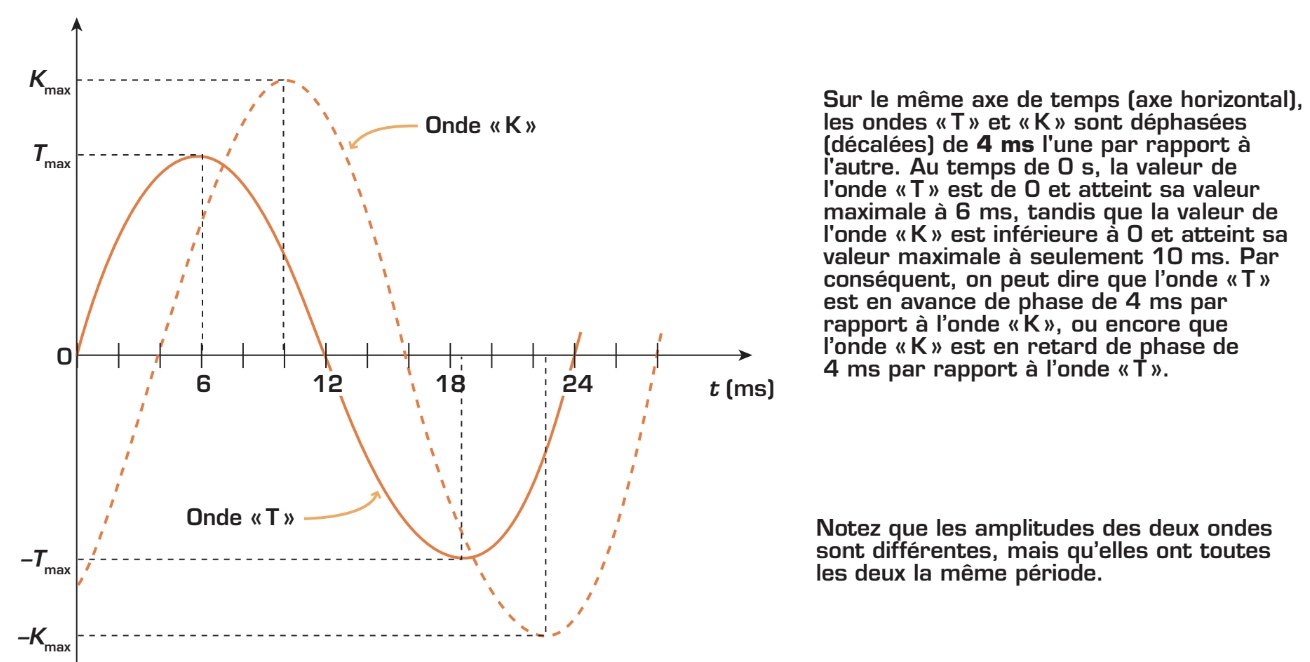
Le déphasage est le terme général utilisé pour désigner le décalage entre deux ondes. Cependant, l’utilisation des expressions «avance de phase» et «retard de phase» permet de préciser la relation de phase entre deux signaux. Notez que la relation de phase peut exister entre deux tensions ou deux courants, ou entre une tension et un courant.
Angle de phase
Lorsque la bobine de l’alternateur fait un tour complet dans le champ magnétique, un cycle de tension de forme sinusoïdale est produit. Ce cycle correspond toujours à 360° (ou 2π radians). Ainsi, le déphasage entre deux ondes peut non seulement être exprimé en temps, comme dans l'exemple précédent, mais aussi en degrés (ou en radians). Lorsque le déphasage est exprimé en degrés (ou en radians), il est appelé «angle de phase». Observez ci-dessous un angle de phase de 90° entre deux ondes.
Sachez qu’il est possible de convertir le temps en degrés en utilisant simplement la «règle de trois» ou le «produit croisé», car contrairement à l’amplitude, qui suit une courbe sinusoïdale, le temps, lui, a une relation linéaire avec l’angle de phase. Si on considère à nouveau le déphasage entre deux ondes sinusoïdales illustré précédemment, on observe que l’onde «K» est en retard de 4 ms par rapport à l’onde «T». Combien ce temps représente-t-il de degrés? Pour trouver la solution, il suffit d’appliquer la règle de trois suivante :

Cette technique est utilisée pour dessiner les vecteurs de phase ou pour calculer la tension instantanée d’une onde. Notez que l’angle de phase correspond au paramètre z de la formule de la valeur instantanée. Portez une attention particulière à sa polarité (signe).
Vecteur de phase
Vous vous doutez bien qu’il n’est pas toujours très pratique de dessiner les ondes sinusoïdales afin de les comparer. Cette tâche devient ardue et complexe lorsque les ondes sont déphasées. Heureusement, il existe une méthode qui permet de simplifier cette opération : elle consiste à dessiner le diagramme vectoriel et fait appel aux vecteurs de phase.
Avant d’aborder de façon plus précise les vecteurs de phase, nous devons rappeler les notions de base relatives aux vecteurs. Un vecteur est une représentation linéaire d’une force physique. En général, cette force peut être un poids ou une vitesse. Dans notre cas, elle peut être l’un des quatre paramètres électriques, soit une tension, un courant, une résistance ou une puissance. Comme illustré ci-dessous, un vecteur est caractérisé par un module (une longueur), un sens et une direction.
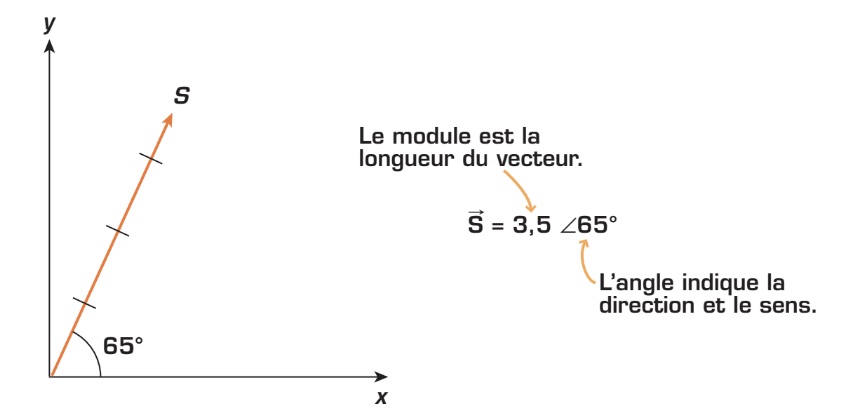
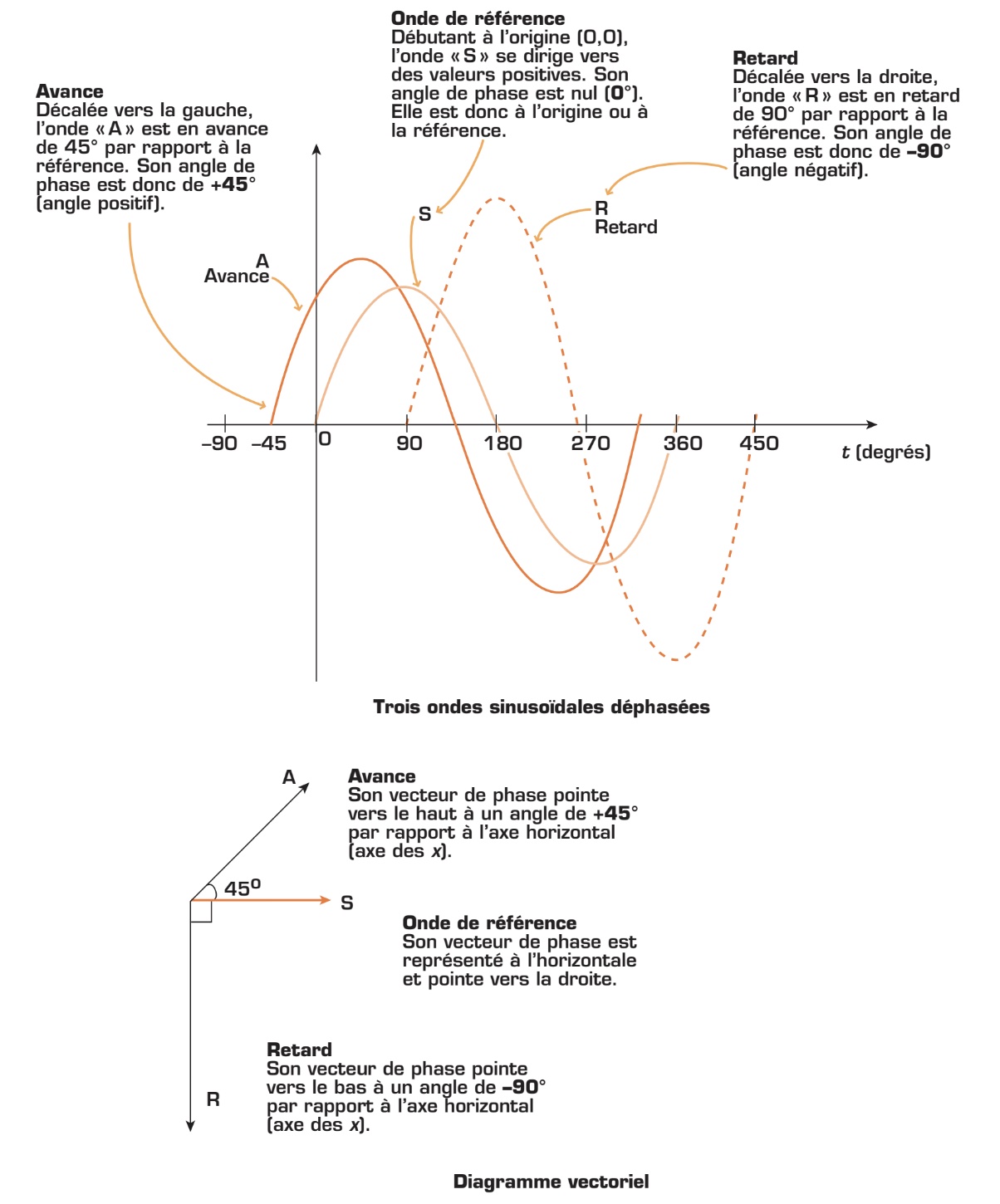
Le vecteur de phase est un vecteur dont la direction correspond à l’angle de phase par rapport à l’origine (axe des x) et dont le module (longueur) correspond à la valeur efficace (tension, courant, puissance) de l’onde. Observez ci-dessous trois ondes sinusoïdales déphasées et leur représentation en vecteur de phase. On désigne cette représentation par les expressions «diagramme vectoriel» ou «diagramme de phase».
Appareils de mesure du courant alternatif
Au cours de vos activités d’électricien, vous serez surtout amené à travailler sur des circuits c.a. Ce sont donc des mesures de tensions et de courants alternatifs que vous effectuerez le plus souvent. Comme vous le savez déjà, le multimètre (ou la pince ampèremétrique) sera l’appareil de mesure qui vous accompagnera dans toutes les situations, qu’il s’agisse de l’installation, de la maintenance ou du dépannage de circuits électriques. L’oscilloscope est également utilisé à l’occasion, principalement pour le dépannage des circuits électroniques et pour la détermination du facteur de puissance des installations électriques. C’est de cet appareil, indispensable à votre formation, dont il sera question dans cette section. Mais, avant de vous le présenter, revoyons quelques aspects importants concernant le multimètre.
Multimètre
Lorsque vous prendrez des mesures de tensions et de courants alternatifs, vous utiliserez un multimètre réglé en position CA/AC. Ainsi, votre appareil indiquera la valeur efficace de l’élément mesuré (Veff ou Ieff).
Cependant, si vous réglez votre appareil en position CC/DC pour mesurer une valeur c.a., il vous indiquera la valeur moyenne de cette onde, soit, dans la plupart des cas, une valeur nulle. Si la mesure en c.c. n’est pas nulle (qu’il s’agisse d’un courant ou d’une tension), cela signifie que vous mesurez une onde c.a. modifiée.
Certains multimètres offrent aussi la possibilité de mesurer directement la fréquence d’une onde sinusoïdale. Notez, toutefois, que cette option est souvent limitée aux seules basses fréquences, inférieures à 400 Hz. Bien que cette option ne soit pas souvent utilisée, elle peut être utile en cas de dépannage de circuits électroniques ou de circuits de moteurs alimentés par des variateurs de vitesse «drive ». En effet, pour faire varier la vitesse d’un moteur en c.a., on doit changer la fréquence de la tension d’alimentation. Vous en saurez davantage sur ce point lorsque vous étudierez les dispositifs électroniques des commandes de moteurs.
Oscilloscope
Comme nous l’avons mentionné précédemment, l’oscilloscope est un appareil de dépannage et de diagnostic qui est surtout utilisé en électronique. Dans le cadre de votre apprentissage, cet appareil de mesure vous permettra de visualiser les ondes sinusoïdales associées au courant alternatif et la forme des divers signaux générés dans les circuits.
Bien que l’oscilloscope soit un appareil volumineux, qui peut vous sembler très complexe, il ne mesure que la tension. Vous pouvez donc le considérer tout simplement comme un gros voltmètre qui affiche la courbe de la tension en fonction du temps. Pour le brancher correctement, vous devrez toujours le relier en parallèle avec l’élément ou la portion du circuit à mesurer, comme vous le feriez avec un voltmètre. Souvenez-vous aussi que l’oscilloscope indique toujours la valeur maximale de la tension.
Résumé
Grâce à l’induction électromagnétique, un alternateur génère une tension alternative de forme sinusoïdale et, par conséquent, un courant de la même forme, le courant alternatif (noté c.a.). Dans ce chapitre, vous vous êtes familiarisé avec la terminologie et les valeurs associées à ces ondes sinusoïdales. La figure ci-dessous en résume les principales caractéristiques. Celles-ci vous seront essentielles pour analyser les circuits alimentés en c.a.
Bien qu’en pratique le multimètre demeure l’appareil de mesure privilégié pour mesurer les tensions et les courants alternatifs, vous avez appris qu’il existe un autre appareil, l’oscilloscope, qui ne mesure que la tension; cet appareil permet cependant de visualiser les ondes sinusoïdales et de les comparer. La maîtrise de ces appareils vous sera essentielle pour bien comprendre le comportement des circuits réactifs alimentés en c.a.