CIRCUITS RÉACTIFS RLC EN C.A.

Les connaissances acquises jusqu’à maintenant vous seront précieuses pour comprendre un autre type de circuit, un peu plus complexe, soit le circuit réactif RLC, qui combine les trois types de charges (résistance, bobine et condensateur).

L’étude du contenu de cette section vous permettra, en premier lieu, de connaître le fonctionnement des circuits RLC dont les composants sont raccordés en série, puis le fonctionnement des circuits dont les composants sont raccordés en parallèle. Sachez, cependant, que le circuit RLC série n’existe pas dans la réalité, mais que les concepts théoriques qui y sont associés vous seront très utiles pour bien comprendre les circuits RLC montés en parallèle, ceux qu’au cours de vos activités d’électricien vous rencontrerez très fréquemment. En effet, vous découvrirez, dans ce chapitre, que la performance (en matière de rendement énergétique) des circuits électriques usuels, principalement celle des circuits RL, peut être améliorée si on y ajoute des condensateurs en parallèle.

Circuits RLC série

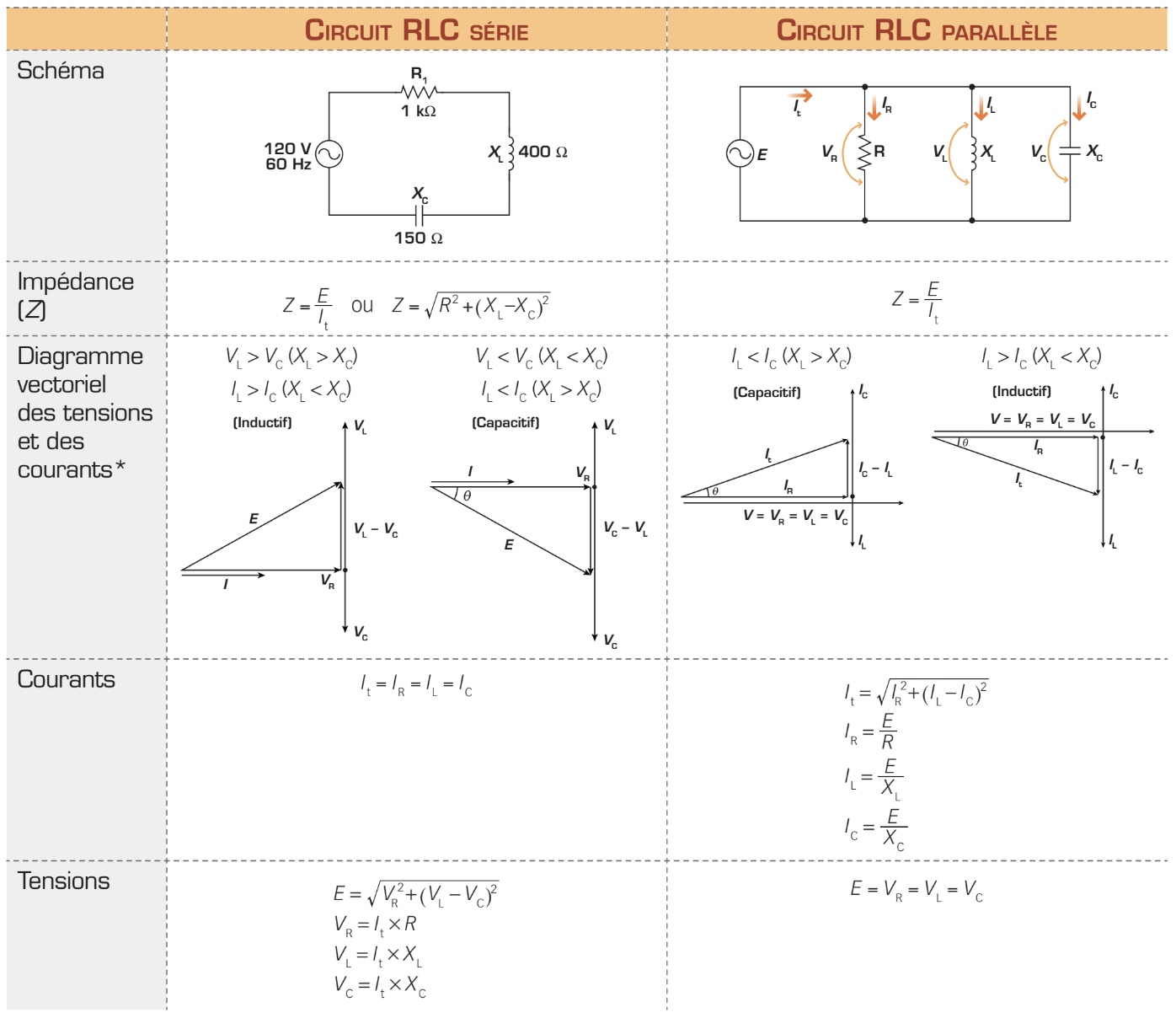
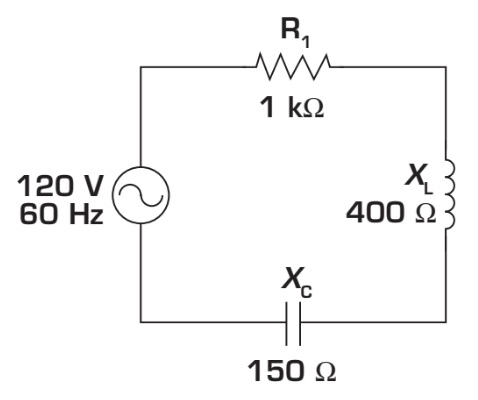
Un circuit RLC série est un circuit électrique dont les trois charges, la résistance, la bobine et le condensateur, sont raccordées les unes à la suite des autres. La figure ci-contre montre un exemple de circuit RLC série. Rappelez-vous que, dans les circuits série, le courant est partout le même et que les tensions aux bornes de chacun des éléments sont différentes. Examinons cela de plus près.

Impédance du circuit RLC série

L’impédance est la mesure de l’opposition totale d’un circuit au passage d’un courant alternatif. Elle peut être calculée à l’aide de deux méthodes.

Méthode 1 : Comme dans tous les circuits réactifs à c.a., l’impédance (Z) d’un circuit RLC série peut être définie, selon la loi d’Ohm, par le rapport entre la tension de source (E) et le courant total débité par cette dernière (It) :

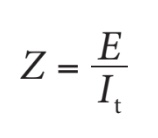
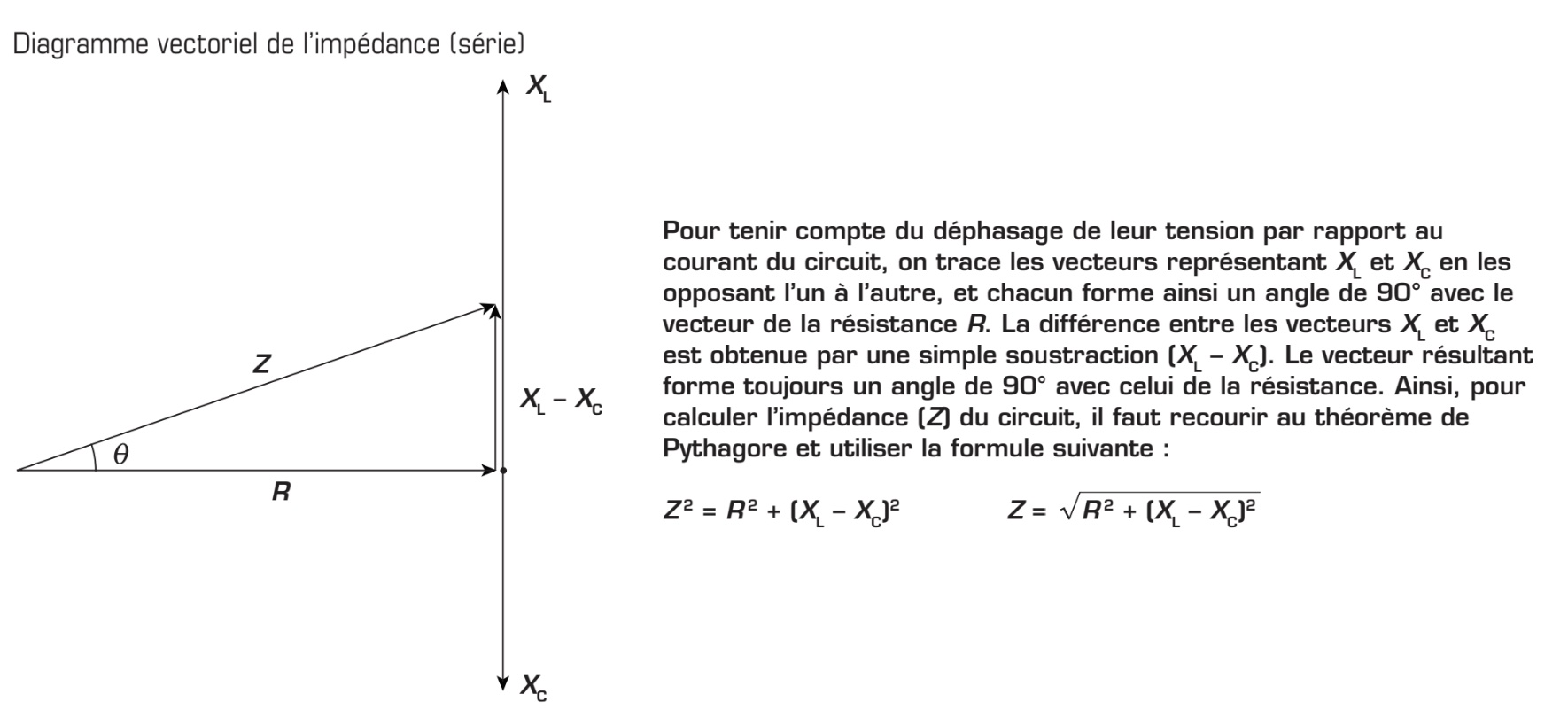
Méthode 2 : L’impédance d’un circuit RLC étant la combinaison de la résistance (R), de la réactance inductive (XL) et de la réactance capacitive (XC), elle peut également être déterminée à l’aide d’un diagramme vectoriel.

Tensions du circuit RLC série

Étant donné que, dans un circuit en série, le courant est partout le même (It = IR = IL = IC), on peut calculer la tension aux bornes de chacune des charges R, L et C en appliquant la loi d’Ohm à l’aide des formules suivantes :

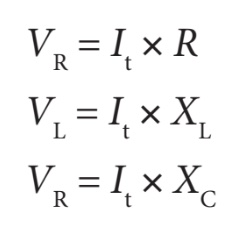
la tension de la résistance (VR) est en phase avec le courant débité par la source (It);
la tension de la bobine (VL) est en avance de phase de 90° par rapport au courant (It);
la tension aux bornes du condensateur (VC) est en retard de phase de 90° par rapport au courant (It).

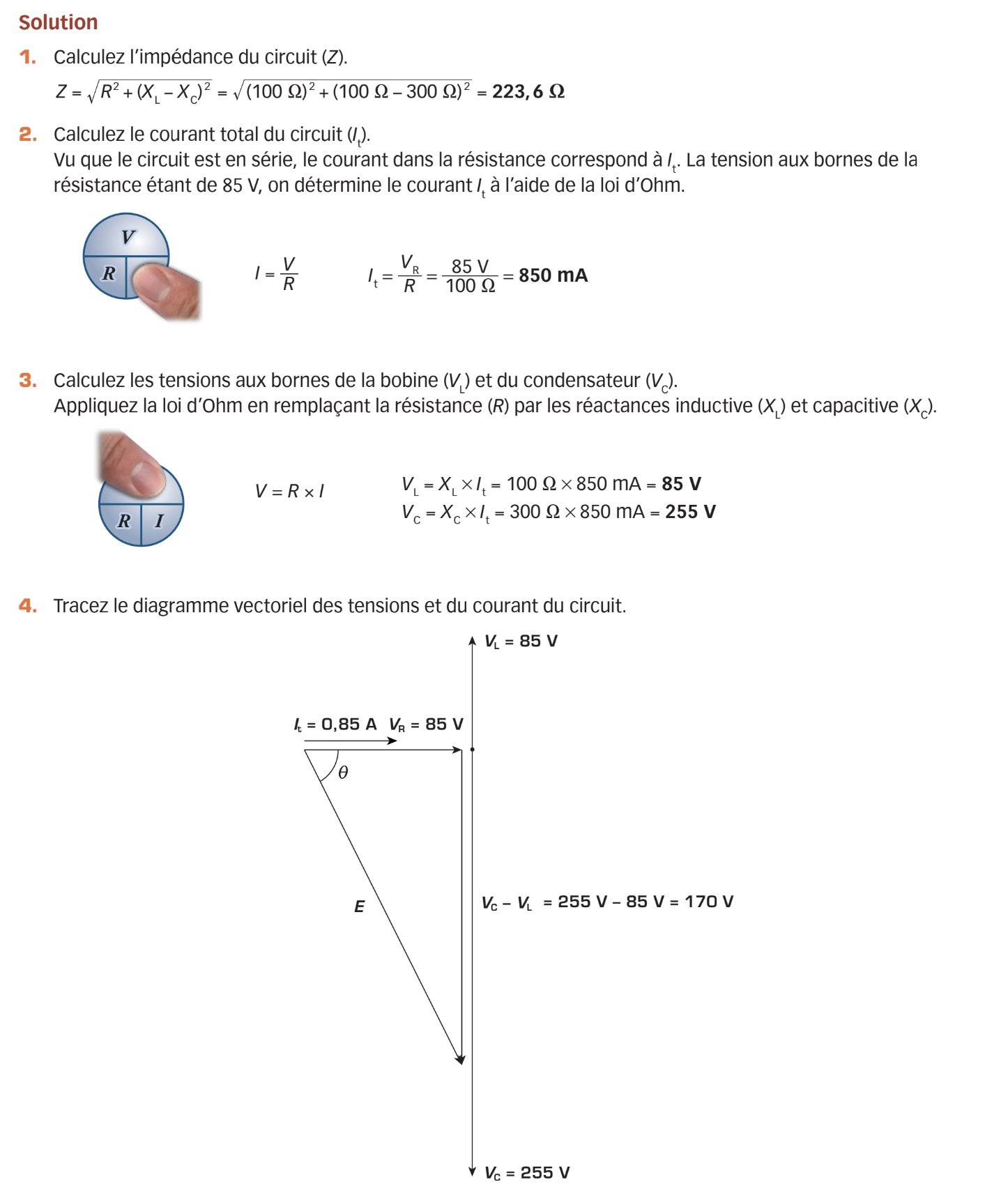
La relation de phase entre ces tensions et le courant du circuit RLC série peut être représentée par un diagramme vectoriel. Comme le montre le diagramme de la page suivante, le sens de ce dernier dépend de la relation de grandeur entre les tensions VL et VR, donc de XL et de XC.

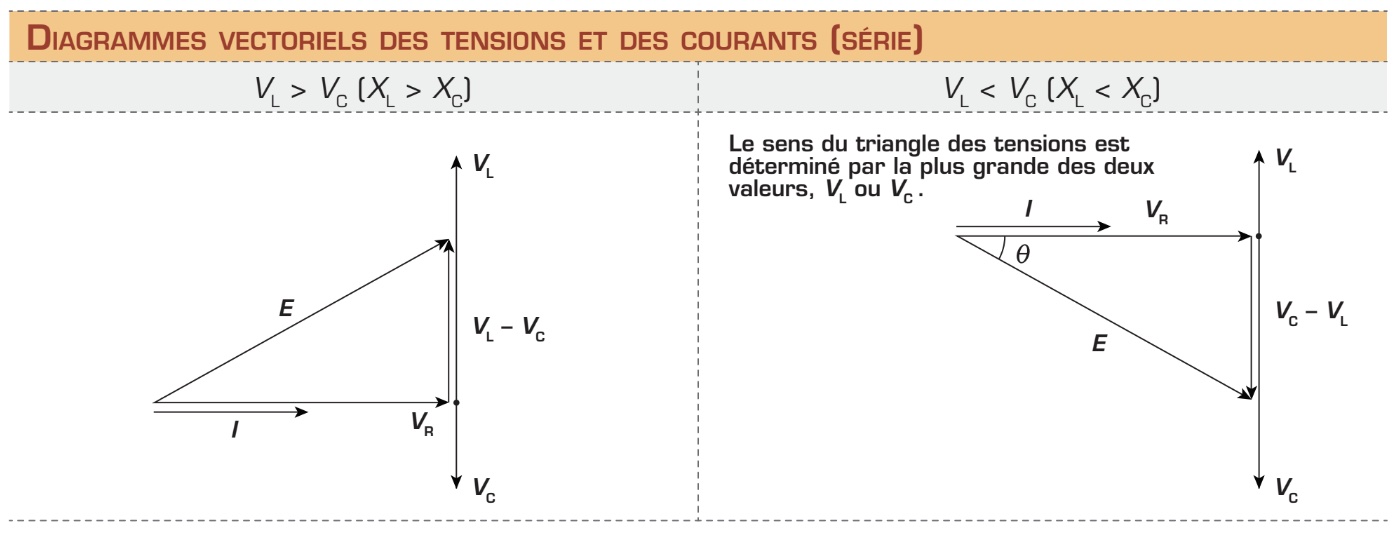
À cause du déphasage entre les tensions, il est impossible d’obtenir leur somme par une simple addition. Pour déterminer la tension de source E, il faut recourir à la méthode d’addition vectorielle et au théorème de Pythagore. L’équation obtenue est la suivante :

Pour bien orienter les vecteurs des tensions et des courants des circuits RLC, vous pouvez utiliser le même truc astucieux qui vous a été présenté pour les circuits RL et RC.

Déphasage entre le courant et la tension de source

En présence d’éléments réactifs (bobines et condensateurs), il y a un déphasage (i) entre la tension de source E et le courant qui circule dans le circuit (It). Si la tension aux bornes de la bobine est plus élevée que la tension aux bornes du condensateur (VL > VC), le circuit RLC se comporte presque comme un circuit inductif RL série. On qualifie alors le circuit RLC de «majoritairement inductif». Le déphasage est positif (angle i situé au-dessus de l’axe des x). Si, au contraire, la tension aux bornes du condensateur (VC) est plus grande que la tension aux bornes de la bobine (VL), le circuit RLC est alors «majoritairement capacitif» et le déphasage est négatif (angle i situé sous l’axe des x).

Pour déterminer le déphasage entre la tension de source et le courant du circuit, on peut appliquer les trois fonctions trigonométriques d’un triangle rectangle (SOHCAHTOA). Ici, nous utiliserons la fonction tangente.

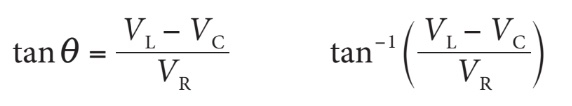
Circuits RLC parallèle

Les circuits RLC en parallèle sont des circuits assez complexes. Cependant, ne vous inquiétez pas, car avec les bases que vous avez acquises jusqu’à présent, vous êtes en mesure de comprendre assez facilement le fonctionnement de ce type de circuit.

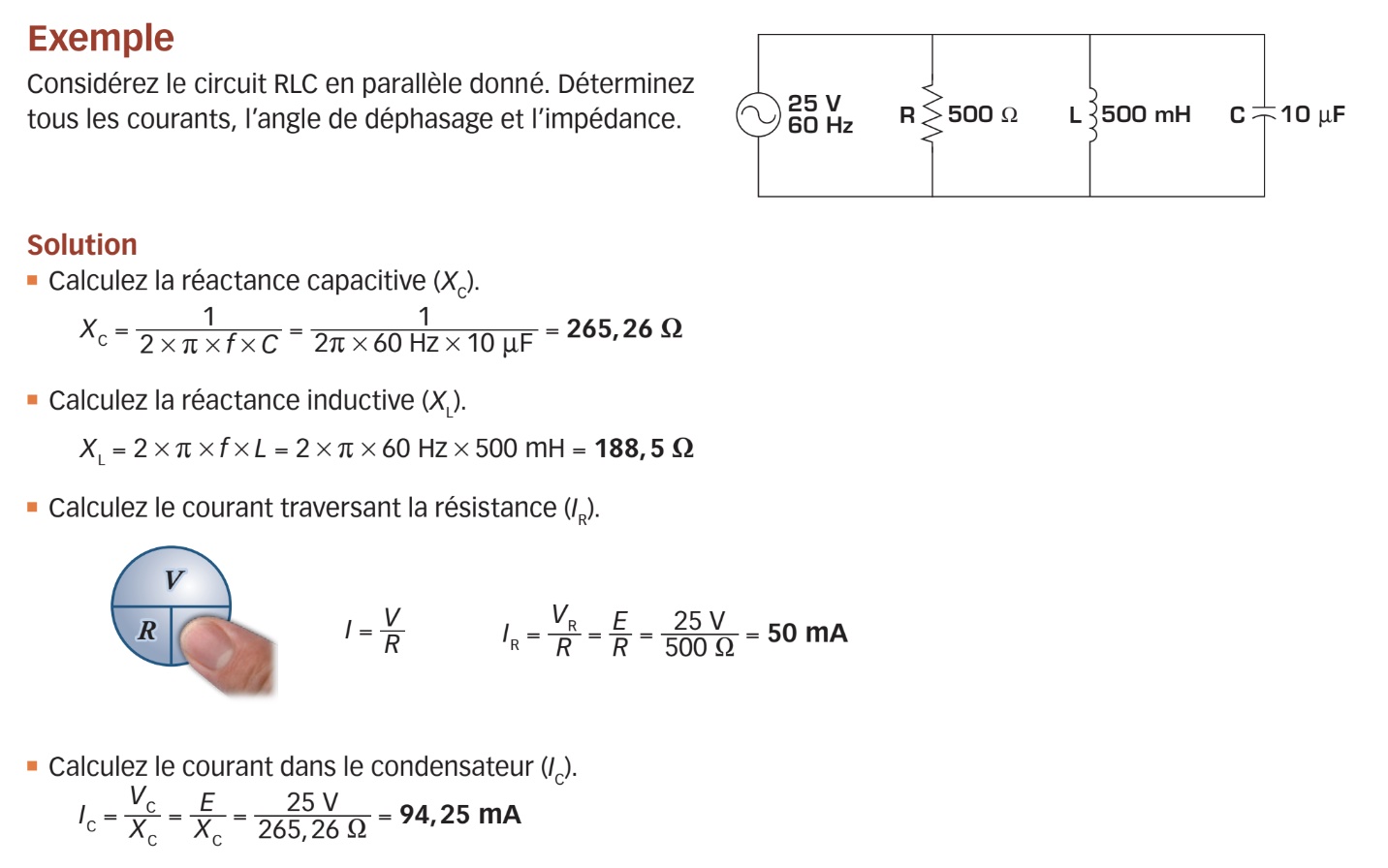
Courants du circuit RLC parallèle

La figure ci-dessous présente un circuit RLC où les trois charges (résistance, bobine et condensateur) sont reliées en parallèle.

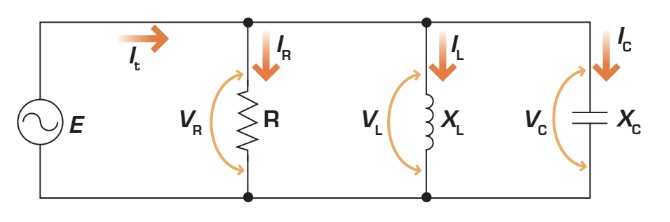
Dans ce type de circuit, la tension est la même aux bornes de chacune des charges et est égale à la tension de source (E = VR = VL = VC). Par contre, le courant dans chacune des charges dépend respectivement de la résistance (R), de la réactance inductive (XL) et de la réactance capacitive (XC). Chaque courant est donc différent et peut être calculé à l’aide de la loi d’Ohm :

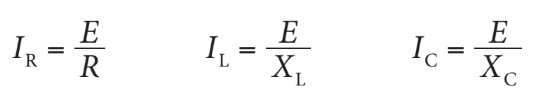
Rappelez-vous que :

le courant de la résistance (IR) est en phase avec la tension de source (E);
le courant de la bobine (IL) est déphasé de –90° (retard de phase) par rapport à la tension de source (E);
le courant du condensateur (IC) est déphasé de +90° (avance de phase) par rapport à la tension de source (E).

Ces relations de phase entre les courants et la tension de source d’un circuit RLC en parallèle peuvent donc être représentées par un diagramme vectoriel. Celui-ci varie selon la relation de grandeur entre les réactances XL et XC.

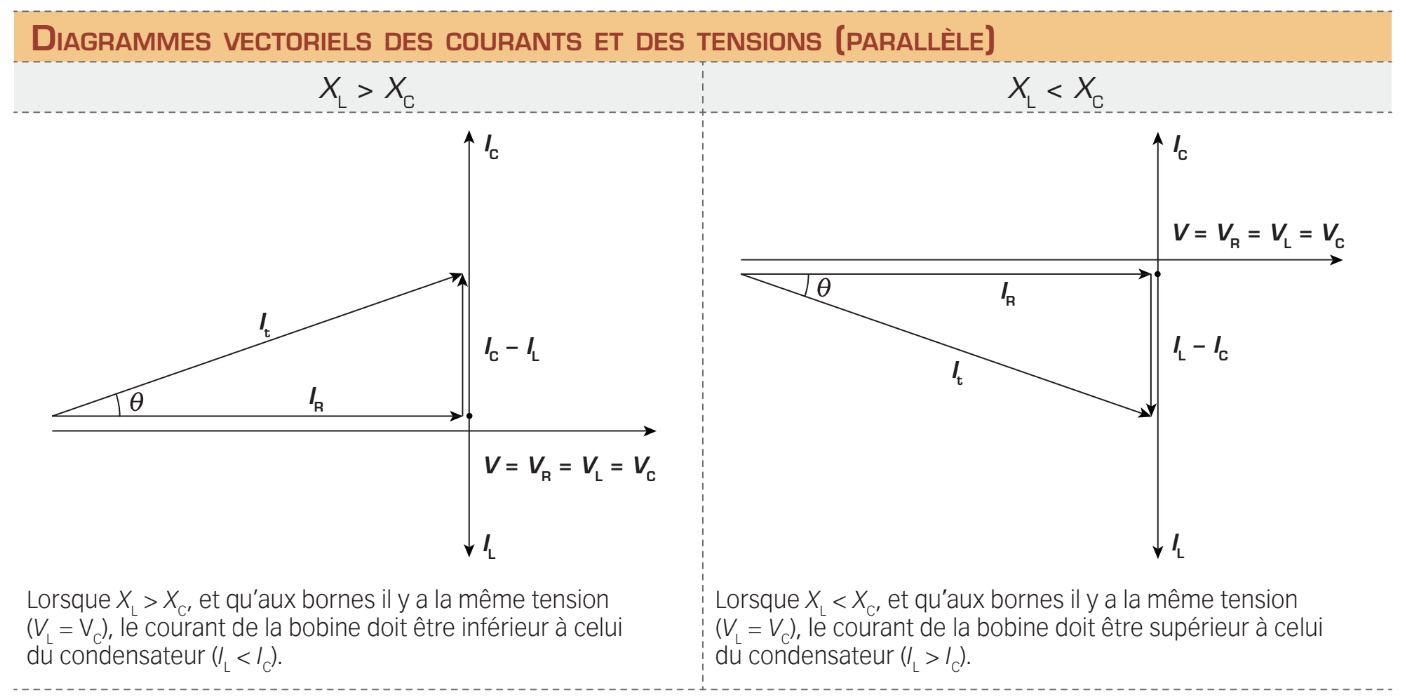
En observant la figure ci-dessus, vous pouvez constater que les courants IL et IC sont en opposition. Pour déterminer le courant réactif final, qui est demandé à la source, vous devez donc soustraire le plus petit de ces courants du plus grand. Comme le montre le diagramme, le sens du triangle qui en résulte est déterminé par le courant réactif le plus élevé. Pour déterminer la valeur du courant total It, qui est fourni par la source, vous devez appliquer le théorème de Pythagore.

Notez que la soustraction des courants (IL – IC) se traduit par une diminution de la demande totale de courant à la source. En effet, les deux éléments réactifs, la bobine et le condensateur, échangent «alternativement» une partie de leur courant, diminuant ainsi la demande à la source.

Impédance du circuit RLC parallèle

Connaissant le courant total fourni au circuit (It) et la tension de source (E), vous pouvez calculer l’impédance (Z) d’un circuit RLC en parallèle en appliquant simplement la loi d’Ohm.

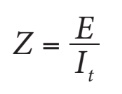
Déphasage entre le courant et la tension de source

En présence d’éléments réactifs (bobines et condensateurs), il y a un déphasage (i) entre le courant (It) et la tension de source (E). Si le courant de la bobine est plus grand que le courant du condensateur (IL > IC), le déphasage est négatif (angle i sous l’axe des x). On parle alors de circuit «majoritairement inductif». À l’inverse, si le courant du condensateur est plus grand que le courant de la bobine (IL < IC), le déphasage est positif et le circuit est alors un circuit «majoritairement capacitif».

Pour déterminer le déphasage entre le courant et la tension de source, on peut appliquer les trois fonctions trigonométriques (SOHCAHTOA). Ici, nous utiliserons la fonction tangente, appliquée sur le triangle des courants.

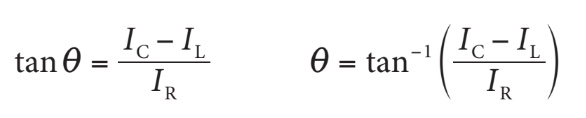
Puissances et facteur de puissance

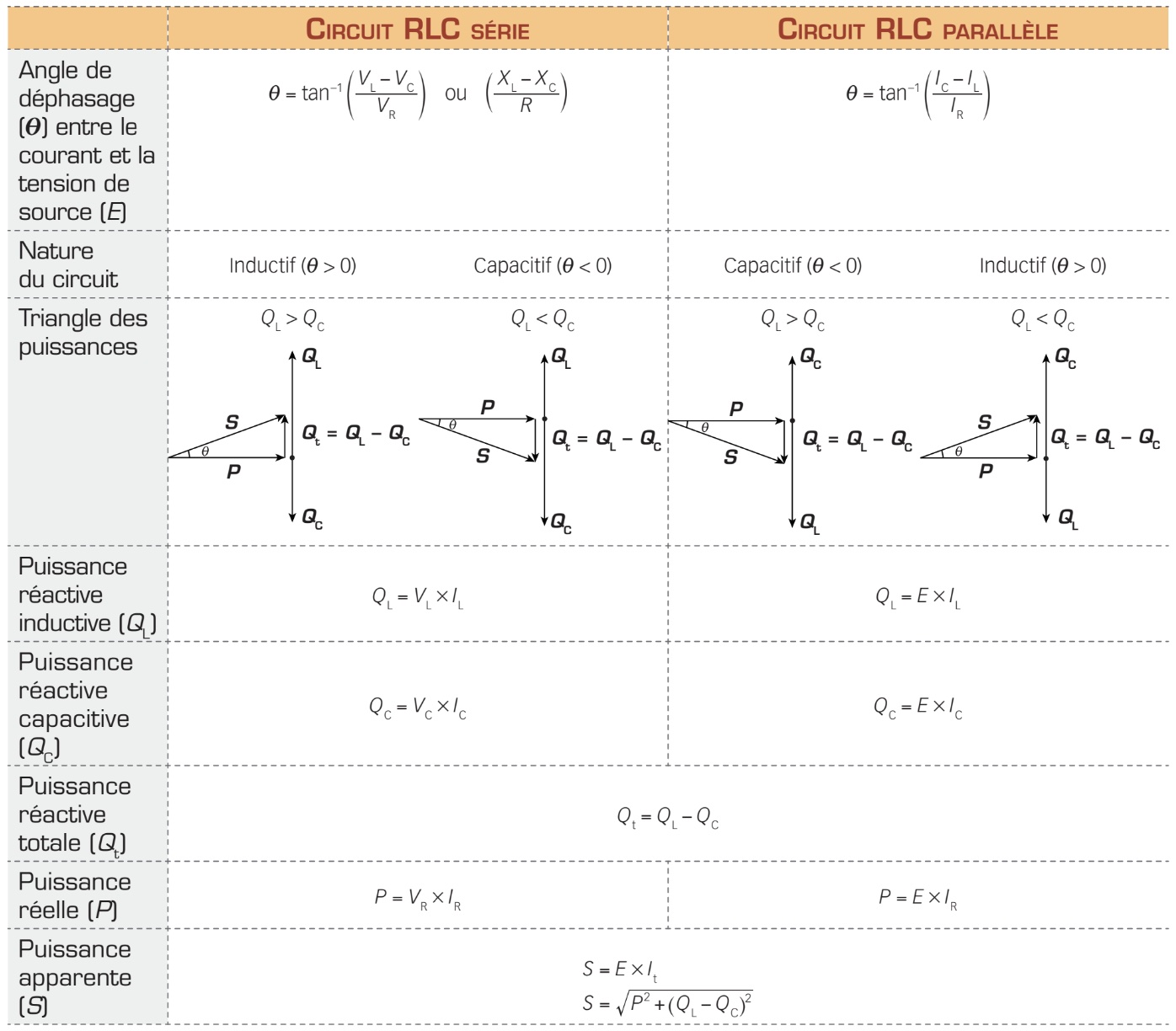
Dans un circuit réactif alimenté en c.a., les puissances sont indépendantes du type de configuration. Un circuit RLC possède donc les trois mêmes types de puissances que l’on trouve dans les circuits RL et RC.

Puissances réactives Contrairement aux circuits RL ou RC, qui ne présentent qu’une seule puissance réactive, les circuits RLC contiennent les deux types, soit la puissance réactive inductive (QL), associée à la bobine, et la puissance réactive capacitive (QC), associée au condensateur. Leur valeur représente toujours le produit de la tension présente aux bornes de l’élément réactif (bobine ou condensateur) multipliée par le courant circulant dans l’élément :

Comme dans un circuit RLC en parallèle, la tension est la même aux bornes de chaque élément réactif (E = VL = VC), on peut donc écrire les formules suivantes :

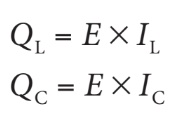
Étant donné qu’il existe simultanément deux charges réactives dans un circuit RLC, la bobine et le condensateur, la puissance réactive totale du circuit (Qt) correspond à la totalité des puissances réactives associées au condensateur et à la bobine. Toutefois, à cause du déphasage entre la tension et le courant dans chacun de ces composants, les puissances réactives de la bobine (QL) et du condensateur (QC) sont directement opposées. Ainsi, en série, le vecteur représentant QL pointe vers le haut et celui de QC pointe vers le bas, tandis qu’en parallèle la situation est inversée. La puissance réactive totale (finale) correspond donc à la différence entre les puissances réactives inductive et capacitive :

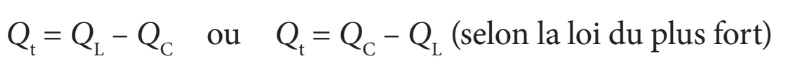
Observez à la page suivante la représentation vectorielle des relations de phase entre la puissance réactive du condensateur (QC) et la puissance réactive de la bobine (QL) selon la relation de grandeur entre ces deux valeurs et la configuration du circuit. Comme dans le cas du courant total, le sens du vecteur représentant Qt est déterminé par la puissance réactive la plus élevée, soit QL ou QC.

Puissance réelle

La puissance consommée par les résistances d’un circuit RLC est réellement absorbée et est convertie en chaleur. Cette puissance peut être calculée à l’aide de la formule suivante :

Puissance réelle consommée par une résistance en watts (W) : P = VR × IR

Notez que, dans le cas d’un circuit RLC en parallèle, on peut également écrire la formule comme suit : P = E × IR.

Puisque la résistance ne crée pas de déphasage, la puissance réelle est représentée à l’horizontale dans le triangle des puissances.

Puissance apparente

La puissance apparente correspond à la puissance totale fournie par la source pour satisfaire l’ensemble des éléments de charge du circuit. Dans un circuit RLC parallèle, la demande de puissance apparente (S) est moins grande que dans les circuits RL et RC, en raison de l’échange de puissance qui a lieu directement entre la bobine et le condensateur. L’équation de la puissance apparente (totale) fournie par la source en voltampères (VA) conserve la même forme, soit : S = E × It

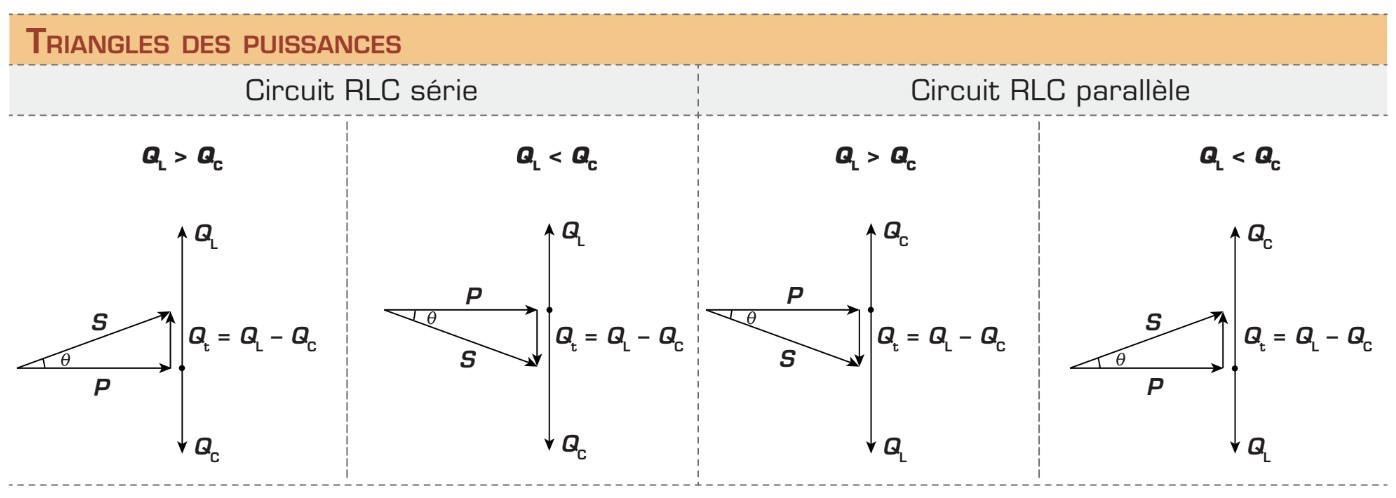
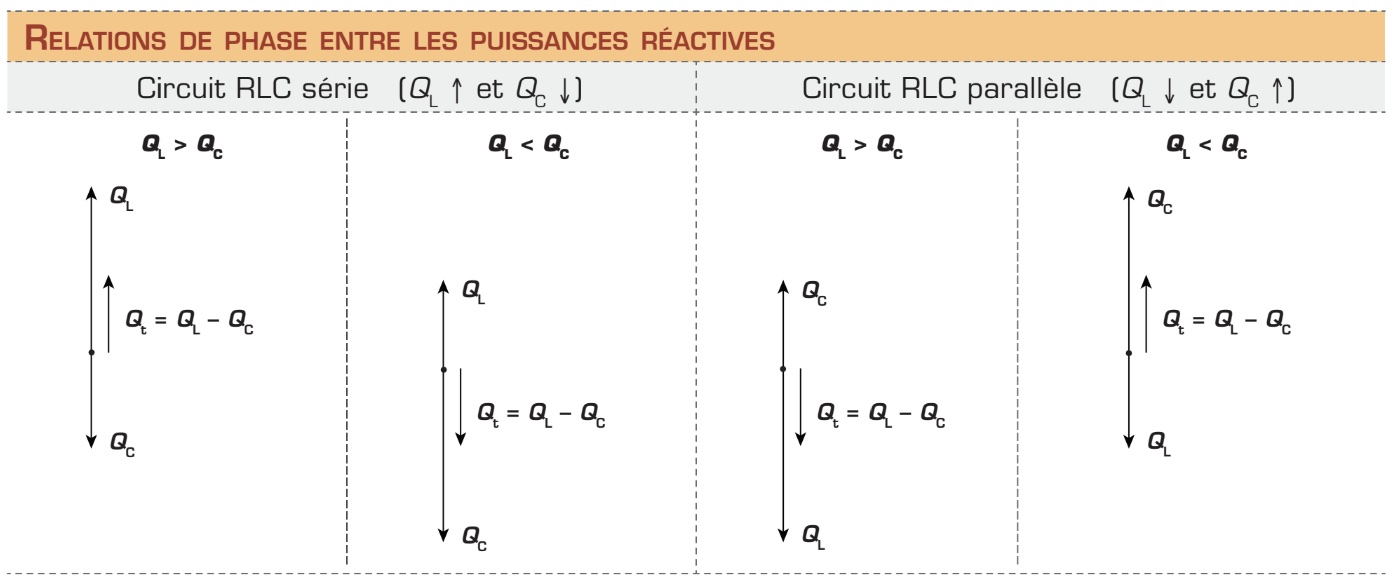
La puissance apparente (totale) peut aussi être déterminée à l’aide du triangle des puissances, tel qu’il est illustré à la page précédente. L’orientation du triangle des puissances dépend à la fois de la configuration du circuit et de la relation de grandeur entre les puissances réactives.

Une fois de plus, vous pouvez constater que le triangle des puissances est un triangle rectangle. Ainsi, la formule de Pythagore s’applique encore une fois et la puissance apparente (S) peut donc être calculée avec la formule suivante :

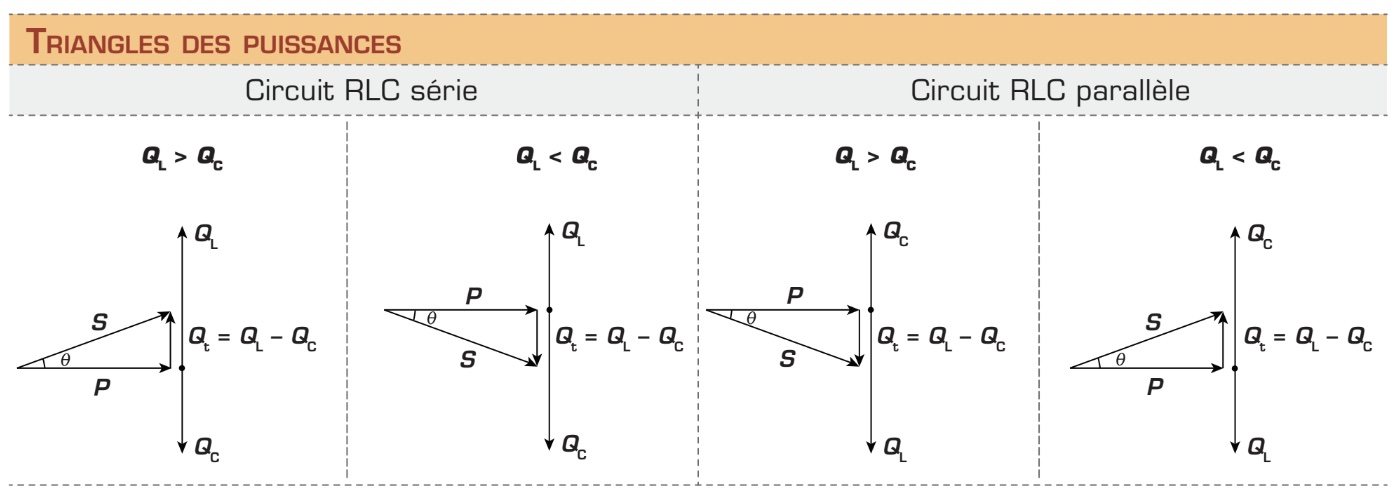
En observant la figure ci-dessus, vous pouvez également constater que plus la puissance réactive totale (Qt) est petite (plus QL est près de QC), plus la puissance apparente (S) sera petite, donc moins la source aura à fournir de puissance. À la limite, lorsque QL est égale à QC (QL = QC), la source ne fournit que la puissance nécessaire pour satisfaire la puissance réelle (S = P). C’est la meilleure des situations, car l’énergie demandée à la source est totalement utilisée pour effectuer un travail (FP = 100 %).

Facteur de puissance

Le circuit RLC offre l’avantage d’être plus performant sur le plan énergétique que le circuit RL. Ainsi, ce type de circuit présente généralement un meilleur facteur de puissance qu’un circuit RL simple.

Comme vous l’avez vu précédemment, on détermine le facteur de puissance (FP) à l’aide de l’une des deux formules suivantes :

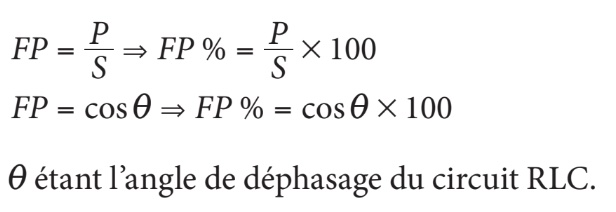
Dans tous les cas, il est indispensable de bien spécifier le type du facteur de puissance, inductif ou capacitif, selon la relation de grandeur entre QL et QC. Dans un circuit RLC série où QL > QC, la puissance apparente (S) est représentée par un vecteur situé au-dessus de l’axe des x (angle i positif). Le facteur de puissance dans un tel circuit est un facteur de puissance inductif. Par contre, dans un circuit RLC série où QL < QC, la puissance apparente (S) se retrouve sous l’axe des x (angle i négatif); le facteur de puissance est alors un facteur de puissance capacitif. Dans les circuits RLC parallèle, la situation est inversée.

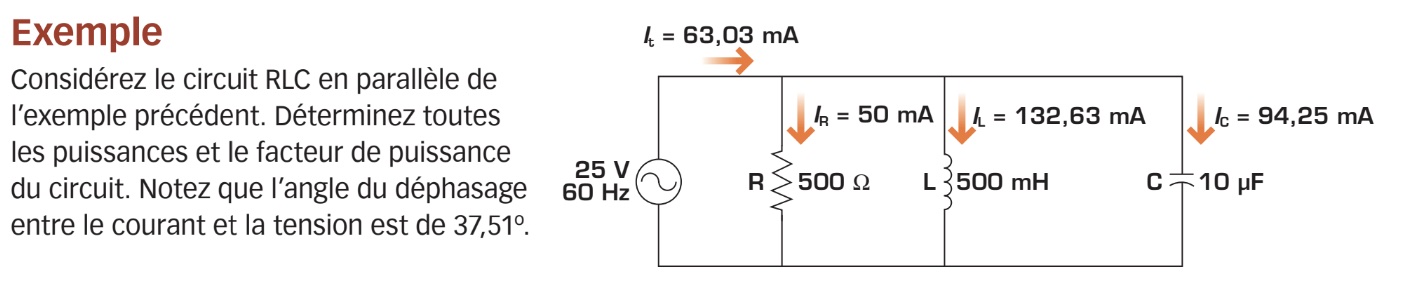
Correction du facteur de puissance

Il a été mentionné précédemment qu’un facteur de puissance trop faible est indésirable dans un circuit électrique. En effet, dans un tel cas, la source doit fournir beaucoup d’énergie, en ce qui a trait au courant et à la tension, pour fournir au circuit une puissance apparente dont seule une partie est consommée par le circuit (puissance réelle). En raison de l’effet inductif des bobines des moteurs, la plupart des circuits électriques industriels sont, dans la pratique, principalement inductifs, et la valeur de leur facteur de puissance est plus petite que l’unité (FP < 1). De là vient la notion de correction du facteur de puissance, qui consiste à modifier le circuit pour ramener son facteur de puissance le plus près possible de l’unité, soit FP = 1 (ou 100 %).

Aussi, si l’on veut que le facteur de puissance soit égal à l’unité, il faut que la puissance apparente soit égale à la puissance réelle (S = P). Autrement dit, il faut amener la puissance réactive totale du circuit à zéro (Qt = 0). Dans cette situation, seules les charges résistives consomment le courant de la source, et les charges réactives sont autosuffisantes. Étant donné que la puissance réactive totale d’un circuit correspond à la différence entre la puissance réactive de la bobine et la puissance réactive du condensateur (Qt = QL – QC), et comme la plupart des circuits industriels sont de nature inductive, il est nécessaire d’ajouter au circuit un condensateur afin de pouvoir diminuer la puissance réactive totale du circuit. Cet ajout permettra d’augmenter le facteur de puissance du circuit et de l’amener le plus près possible de l’unité.

Notez que, dans la pratique, la correction du FP par l’ajout d’un condensateur en série est rarement utilisée, car celui-ci a le désavantage de provoquer l’augmentation du courant. La façon la plus courante de corriger le facteur de puissance est donc d’ajouter un condensateur en parallèle. L’exemple suivant montre une méthode de calcul pour corriger le facteur de puissance d’un circuit partiellement inductif en y ajoutant un condensateur raccordé en parallèle.

Corriger le facteur de puissance

Un condensateur ou un banc de condensateurs en parallèle sont souvent ajoutés pour corriger le FP des installations industrielles contenant de nombreuses charges inductives (moteurs, fours à induction, ballast d’éclairage, etc.). De surcroît, l’intensité du courant à transporter s’en trouve réduite. Ainsi, les lignes électriques aériennes d’Hydro- Québec étant inductives, leur facteur de puissance est corrigé en installant des bancs de condensateurs dans les postes d’interconnexion. Par ailleurs, Hydro-Québec exige que le FP des installations industrielles soit au moins égal à 90 %, sinon des pénalités tarifaires sont imposées.

Ces calculs sont laborieux, n’est-ce pas? Heureusement, il existe une méthode rapide pour trouver la puissance réactive des condensateurs à installer. Si vous connaissez la valeur de la puissance réelle du circuit et son facteur de puissance initial (avant l’ajout du condensateur), le tableau qui suit permet de déterminer la puissance réactive capacitive à ajouter pour corriger le circuit. Il suffit alors de multiplier la puissance réelle du circuit par la valeur donnée dans le tableau. Dans l’exemple précédent, les facteurs de puissance initial et désiré du circuit RLC sont respectivement de 75 % et de 90 %. Le tableau donne la valeur de 0,398. La puissance réelle du circuit étant de 9 kW, la puissance réactive du condensateur à installer est donc de :

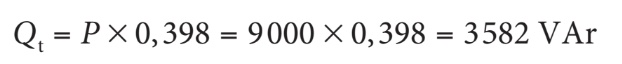
Dans la pratique, des bancs de condensateurs sont placés près de l’entrée électrique des usines. Ceux-ci sont commutés (en circuit/hors circuit) par un dispositif électronique qui « lit » en temps réel le facteur de puissance de l’usine et qui détermine le meilleur agencement de condensateurs à placer dans le circuit d’alimentation pour augmenter le facteur de puissance au plus près de 1 (100 %). Dans certains cas, un moteur asynchrone est ajouté en plus pour tenir le rôle d’un condensateur variable. Il faut alors intégrer aussi une carte électronique et la relier directement à l’entrée de l’usine pour contrôler le moteur selon les besoins de l’alimentation principale.

Résumé

Vous avez étudié les diverses caractéristiques des circuits RLC selon l’agencement des trois charges (résistance, bobine et condensateur). Le tableau ci-après présente les principales caractéristiques des circuits RLC montés en série et en parallèle. Vous avez également appris une chose essentielle pour les électriciens : la façon de corriger le facteur de puissance (FP). En ramenant le facteur de puissance à une valeur très proche de l’unité (ou de 100 %), la correction permet d’accroître la performance des installations électriques. Puisque la plupart de ces installations sont de nature inductive, la méthode de correction du facteur de puissance la plus fréquente consiste à ajouter un ou plusieurs condensateurs raccordés en parallèle ; cette méthode offre en plus l’avantage de réduire le courant total du circuit.