CIRCUITS RÉACTIFS RL ET RC EN C.A.

Vous savez maintenant qu’il existe trois types différents de charges, soit les charges résistives, les charges inductives et les charges capacitives. Dans les circuits c.a., les bobines et les condensateurs se comportent de façon réactive; c’est ce type de comportement que vous étudierez dans cette section.

Vous découvrirez ainsi de nouveaux concepts fondamentaux comme l’impédance, la réactance inductive, la réactance capacitive et les puissances réactives. Étant donné que, dans la plupart des circuits que vous rencontrerez, les charges réactives sont associées à une charge résistive (résistance), il est essentiel d’étudier leur interaction dans un circuit. Quel est l’effet total de ces composants sur la circulation du courant alternatif? Quelles sont les relations entre la tension appliquée et le courant du circuit? Quelle est la puissance totale qui doit être fournie au circuit? Quel est le rendement électrique de ces circuits réactifs? Ce chapitre répondra à toutes ces questions. Pour commencer, nous nous limiterons aux seuls circuits réactifs inductifs RL (résistance et bobine) et capacitifs RC (résistance et condensateur). Le prochain chapitre sera consacré à des circuits un peu plus complexes qui combinent les trois charges (résistance, bobine et condensateur), les circuits RLC.

Comportement de la bobine en c.a.

Une bobine ne se comporte pas de la même manière dans un circuit c.c. et dans un circuit c.a. En effet, dans un circuit c.a., son comportement se rapproche beaucoup de celui de la résistance. Bien que la bobine soit toujours caractérisée par son inductance (L), de nouveaux concepts doivent être utilisés lorsqu’elle est traversée par un courant alternatif.

Réactance inductive

Une bobine s’oppose aux variations de l’intensité du courant. Toutefois, dans un circuit c.a., l’intensité du courant change constamment de valeur et la bobine tente de le stabiliser. Ce faisant, elle entraîne un « ralentissement » ou une réduction du courant dans le circuit. Cet effet d’opposition de la bobine au passage du courant alternatif se nomme réactance inductive; son symbole est XL et, tout comme la résistance, son unité de mesure est l’ohm (Ω).

La réactance inductive d’une bobine peut être calculée par la formule suivante :

Notez que la réactance inductive peut être interprétée comme un type de résistance, et souvenez-vous que la loi d’Ohm reste applicable dans les circuits alternatifs. Par conséquent, on peut déterminer la tension ou le courant d’une bobine alimentée en c.a. en appliquant les formules de la loi d’Ohm; on remplace simplement la résistance (R) par l’inductance réactive (XL). V = R × I devient V = XL × I.

Réactance inductive équivalente

La réactance inductive équivalente ou totale d’un circuit peut être calculée à partir de la réactance inductive de chacune des bobines. Pour ce faire, on procède comme s’il s’agissait de résistances.

Ainsi, dans le cas des bobines en série, on additionne les réactances inductives individuelles :

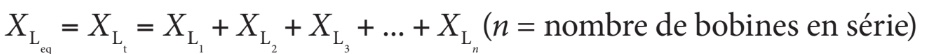
Dans le cas des bobines reliées en parallèle, on calcule la réactance inductive équivalente avec la formule des inverses :

Enfin, s’il s’agit d’un circuit mixte, on calcule la réactance inductive équivalente en utilisant les formules précédentes selon l’agencement des inductances.

Notez, par ailleurs, que la réactance inductive équivalente peut également être calculée à partir de l’inductance équivalente (L eq) du circuit en appliquant la formule suivante :

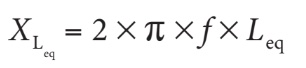
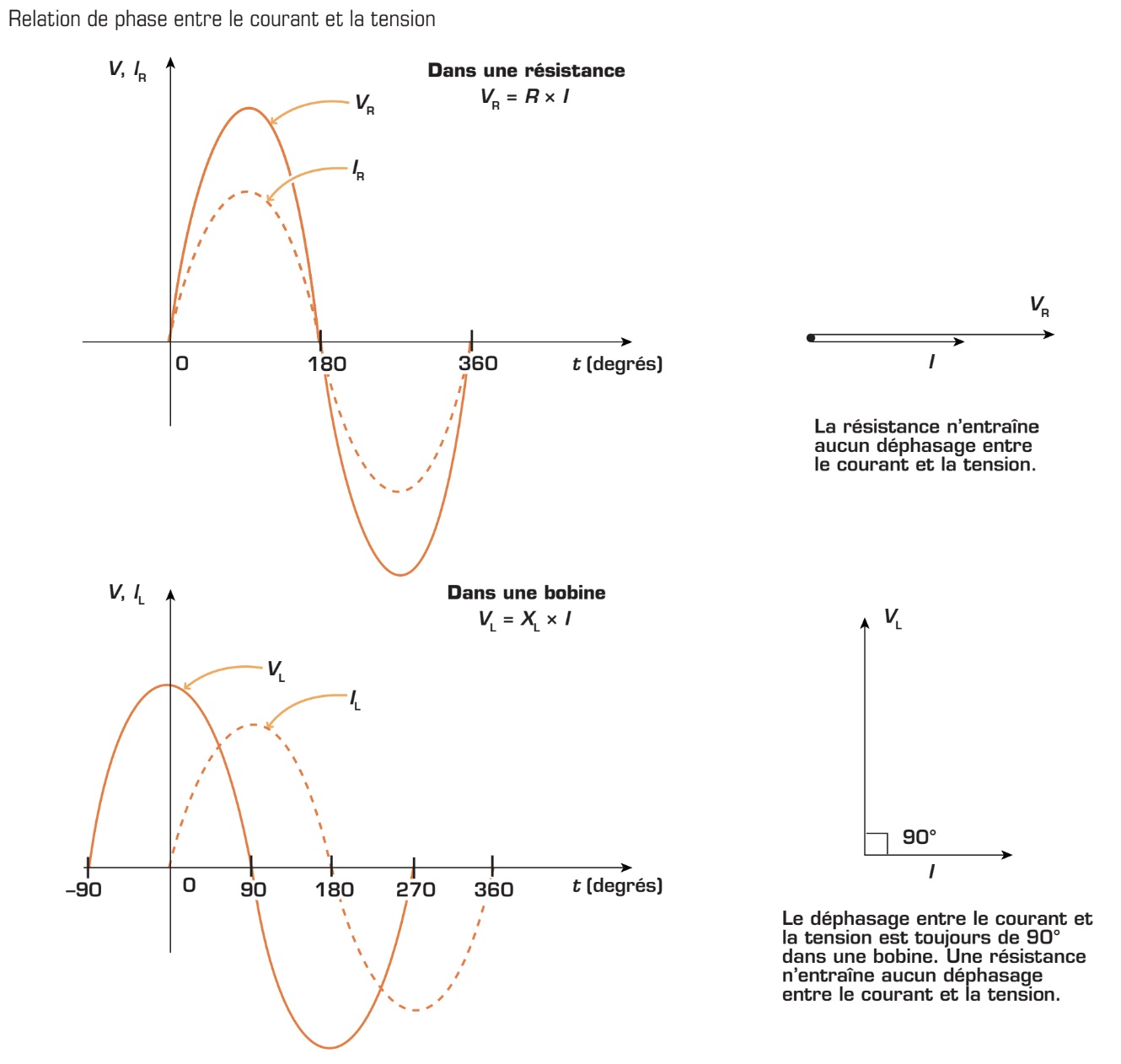
Déphasage du courant

Bien que la bobine ait un comportement semblable à la résistance dans les circuits c.a., son opposition aux variations du courant se traduit par un déphasage entre le courant et la tension. En effet, puisque la bobine s’oppose à toute variation du courant qui la traverse, le courant ne peut parvenir à sa valeur maximale en même temps que la tension appliquée à ses bornes. Ainsi, on observe toujours un retard de phase de 90º du courant (IL) par rapport à la tension aux bornes de la bobine (VL).

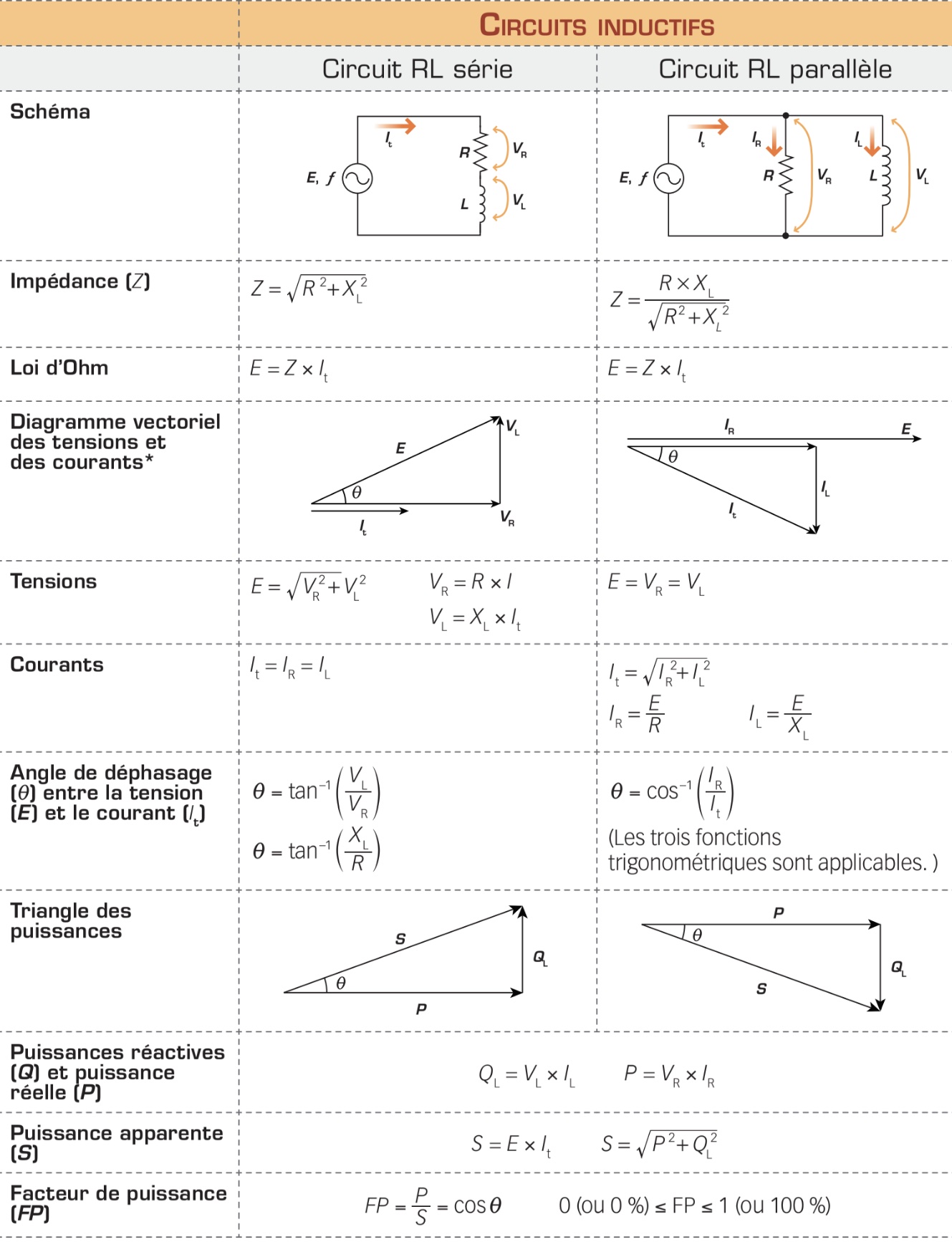
Circuits inductifs RL

Les bobines sont surtout utilisées dans la fabrication des moteurs, des transformateurs, des ballasts et des relais. Attention : bien que ces charges soient inductives, elles possèdent aussi une résistance propre, selon le diamètre et la longueur des fils conducteurs utilisés pour l’enroulement. Ainsi, une charge inductive n’est jamais «pure» et possède toujours une certaine résistance à cause de ses fils. Dans ce cours, nous négligerons toutefois la résistance de la bobine. Notez que les circuits contiennent rarement uniquement des bobines; celles-ci sont généralement raccordées à une ou plusieurs résistances). Les circuits formés par des bobines et des résistances portent le nom de «circuits RL».

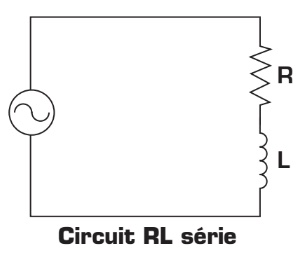
Circuit RL série

Un circuit RL série est composé d’une résistance reliée en série à une bobine. L’interaction de ces deux éléments dans les circuits alimentés en c.a. conduit à l’étude de nouveaux concepts.

Impédance du circuit RL série

L’impédance est l’équivalent de la résistance équivalente ou totale dans un circuit c.a. Elle représente donc l’opposition totale au passage du courant alternatif dans un circuit électrique. Son symbole est la lettre majuscule Z en italique et son unité de mesure est l’ohm (Ω).

Selon les paramètres connus, deux méthodes peuvent être utilisées pour déterminer l’impédance Z d’un circuit RL série.

Méthode 1 : Calcul de l’impédance à l’aide de la loi d’Ohm

Méthode 2 : Calcul de l’impédance totale à l’aide d’un diagramme vectoriel.

Si vous connaissez la valeur de la résistance (R) et celle de la réactance inductive (XL) du circuit RL, vous pouvez calculer la valeur de l’impédance en représentant la relation entre R et XL par un diagramme vectoriel. Faites bien attention de ne pas additionner directement la valeur de la résistance à celle de la réactance inductive.

L’impédance d’un circuit RL série est la somme vectorielle de la résistance (R) et de la réactance inductive (XL). Cette relation se traduit par l’équation suivante :

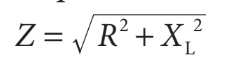
Courant du circuit RL série

Pour calculer le courant unique du circuit RL série, la loi d’Ohm reste pertinente. Cependant, n’oubliez pas d’utiliser la valeur de l’impédance (Z) du circuit, et non la valeur de la résistance (R) ou de la réactance inductive (XL).

Tensions du circuit RL série

Comme dans tous les circuits série, la tension de source d’un circuit RL série est répartie dans chacune des charges, soit entre la résistance (R) et la bobine (L). Par contre, cette répartition de tension se fait vectoriellement. En d’autres termes, la tension de la source (E) est égale à la somme vectorielle de la tension aux bornes de la résistance (VR) et de celle aux bornes de la bobine (VL). La figure ci-dessous montre les relations entre le courant (qui est en tout point identique, car c’est un circuit série) et les différentes tensions du circuit.

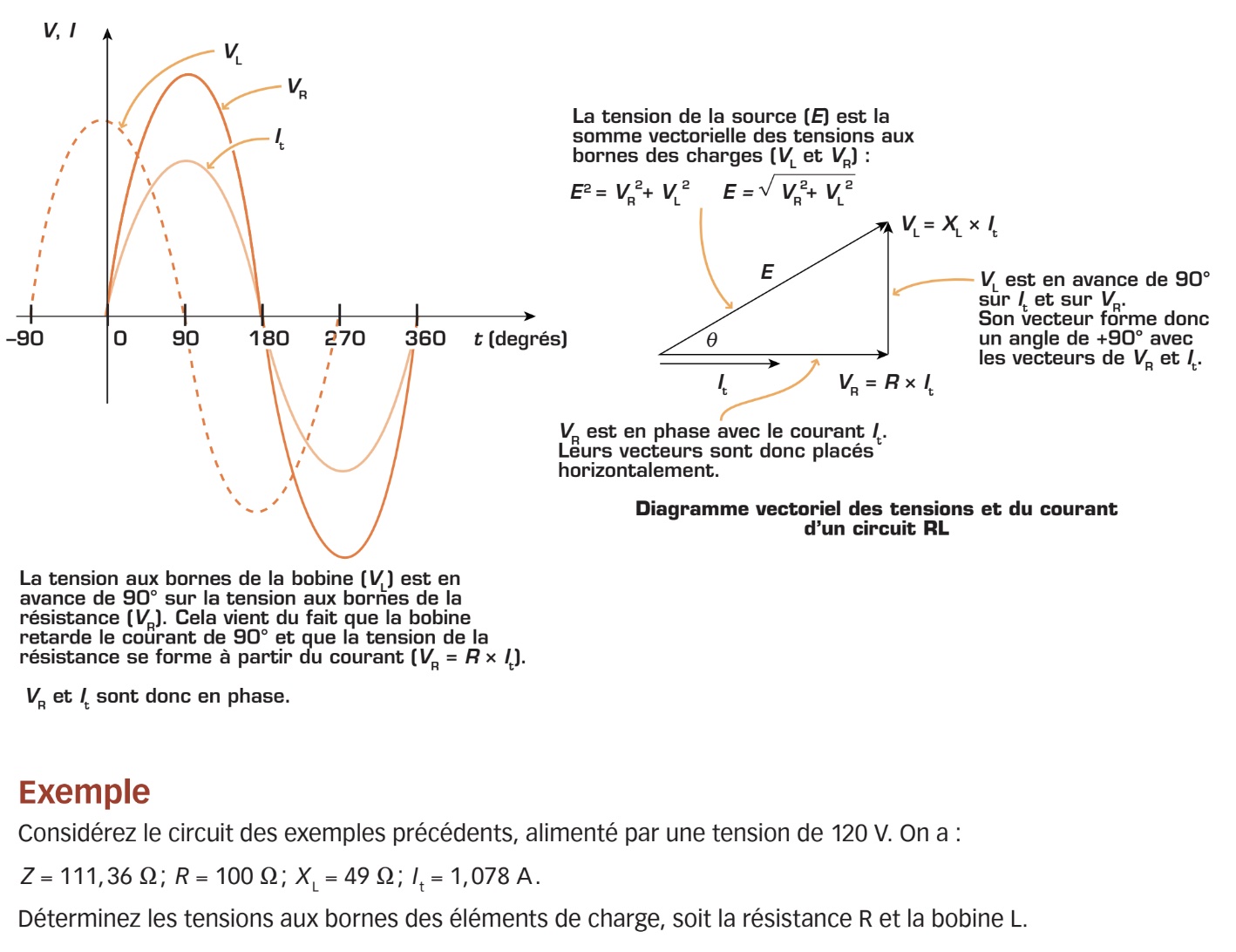
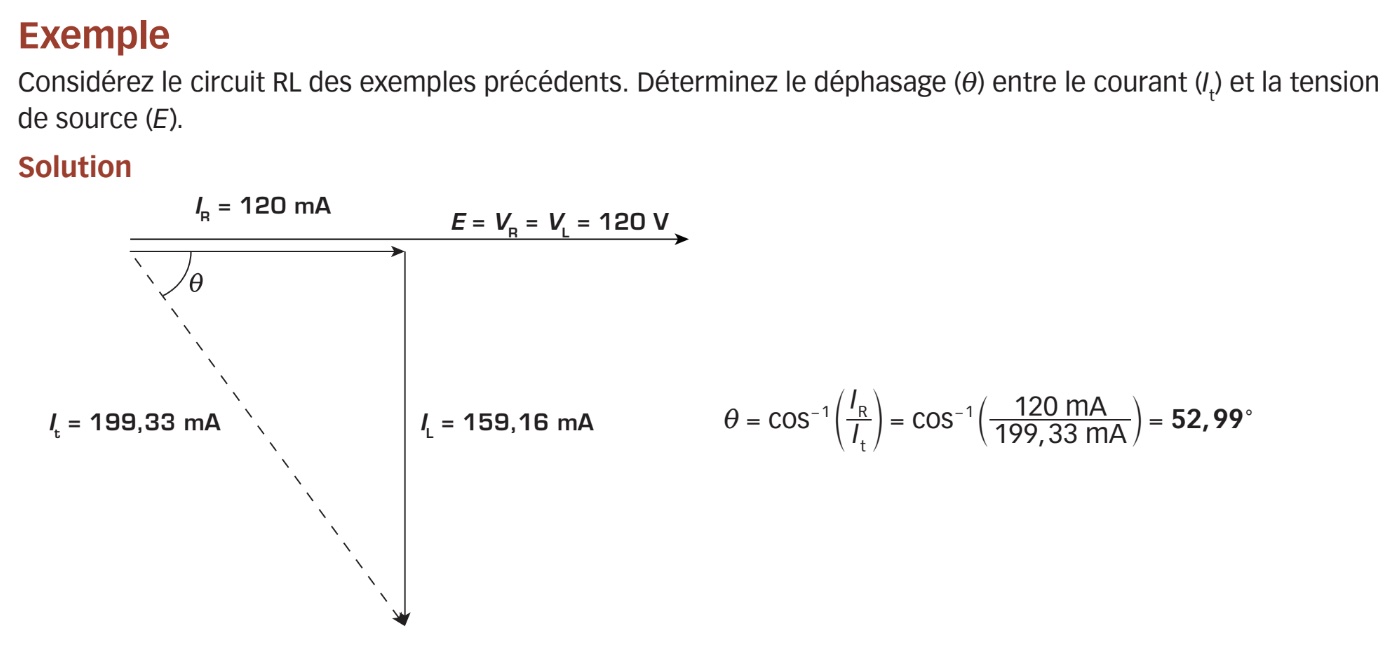
Déphasage entre le courant et la tension de source du circuit RL série

Comme vous l’avez constaté, il existe un déphasage entre le courant It et la tension de source E. Sur le diagramme vectoriel, ce déphasage est représenté par l’angle formé par le vecteur de la tension de source (E) et celui du courant (It, en phase avec VR). Cet angle correspond à l’angle formé par le côté adjacent et l’hypoténuse du triangle rectangle. Pour le calculer, on doit donc appliquer l’une des trois fonctions trigonométriques (SOHCAHTOA). Dans ce cas, nous utiliserons la fonction tangente.

Plus simplement, on peut dire que le diagramme vectoriel de l’impédance est proportionnel à celui de la tension. Ainsi, l’angle présent entre le côté adjacent et l’hypoténuse du triangle de l’impédance est le même que celui présent dans le triangle des tensions.

Circuit RL parallèle

Les circuits en parallèle sont les plus répandus. Un circuit RL en parallèle se compose d’une bobine reliée en parallèle à une résistance. Le principe du calcul des différents paramètres est similaire à celui prévalant dans le calcul des paramètres d’un circuit RL série. Par contre, étant donné qu’en parallèle la tension est partout la même, c’est donc le diagramme vectoriel des courants qui devra être réalisé pour observer le déphasage.

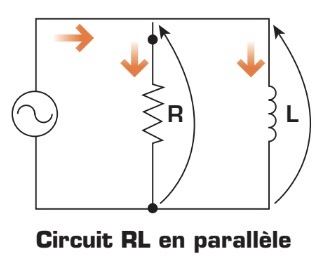
Impédance du circuit RL parallèle

Comme dans le cas des circuits RL série, deux méthodes peuvent être utilisées pour déterminer l’impédance (Z) d’un circuit RL en parallèle, selon les paramètres connus.

Méthode 1 : Calcul de l’impédance à l’aide de la loi d’Ohm

Méthode 2 : Calcul de l’impédance d’un circuit RL en parallèle

Si vous connaissez la valeur de la résistance (R) et celle de la réactance inductive (XL) du circuit, vous pouvez déterminer la valeur de l’impédance (Z). Toutefois, il n’est pas possible de faire un calcul vectoriel dans ce cas (ce qu’on peut faire s’il s’agit d’un circuit RL série). En effet, souvenez-vous que les résistances reliées en parallèle ne s’additionnent pas directement. La formule pour calculer l’impédance (Z) d’un circuit RL en parallèle est la suivante :

Courants du circuit RL parallèle

Vous savez déjà que les circuits en parallèle se caractérisent par des courants différents dans chacune des branches du circuit. Avec le courant total fourni par la source, on distingue donc trois courants différents dans le circuit RL. Chacun de ces courants a une particularité :

le courant qui traverse la résistance (IR) est en phase avec la tension de source (E);
le courant qui traverse la bobine (IL) est en retard de phase de 90° par rapport à la tension de source (E);
le courant total débité par la source (It) est en retard sur sa tension d’un angle de 0° à 90°, selon la répartition de R et de XL

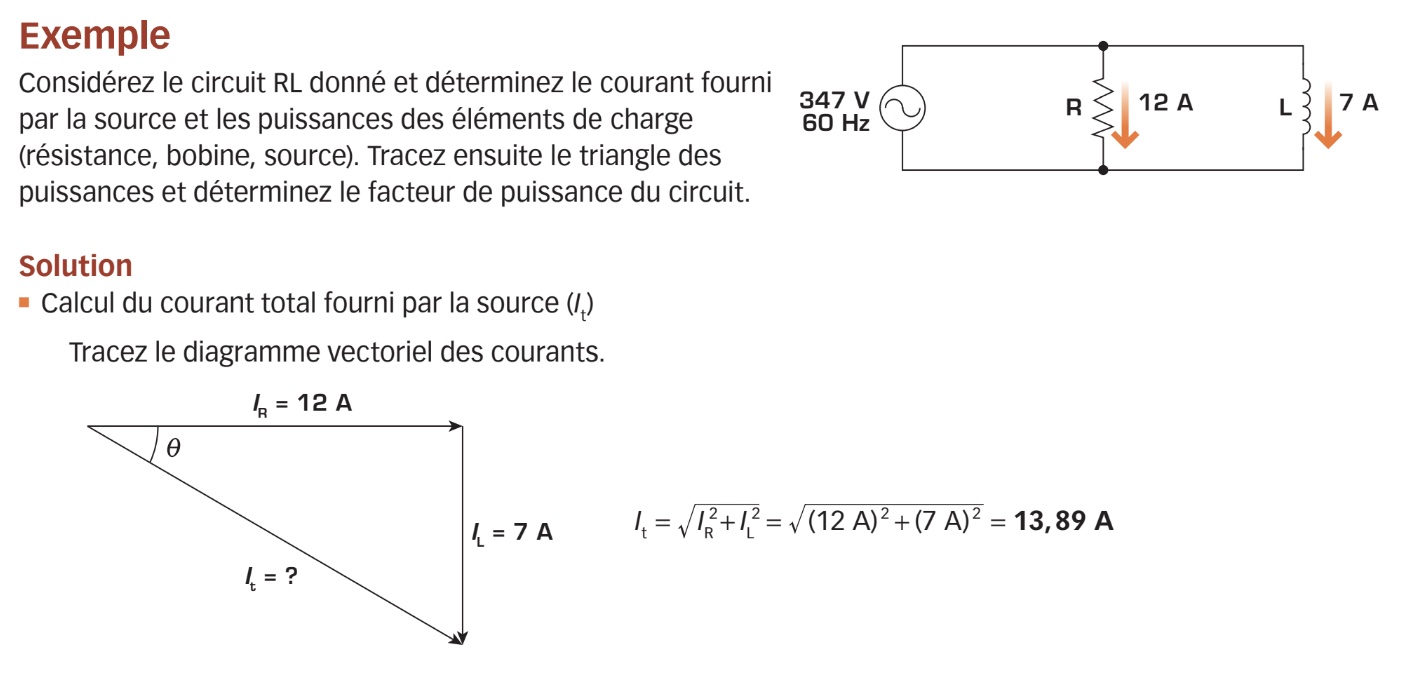
On peut donc en déduire que le courant de la bobine (IL) est en retard de 90° par rapport à celui de la résistance (IR). La figure ci-dessous montre la représentation vectorielle de ces trois courants. Lorsqu’on connaît la valeur des courants de charge, ce diagramme permet de calculer le courant total du circuit (It).

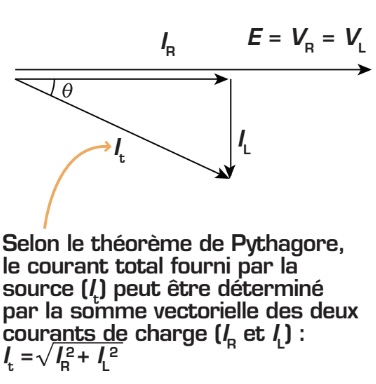
Pour calculer les trois courants circulant dans chacun des éléments (résistance, bobine et source), on peut également appliquer la loi d’Ohm :

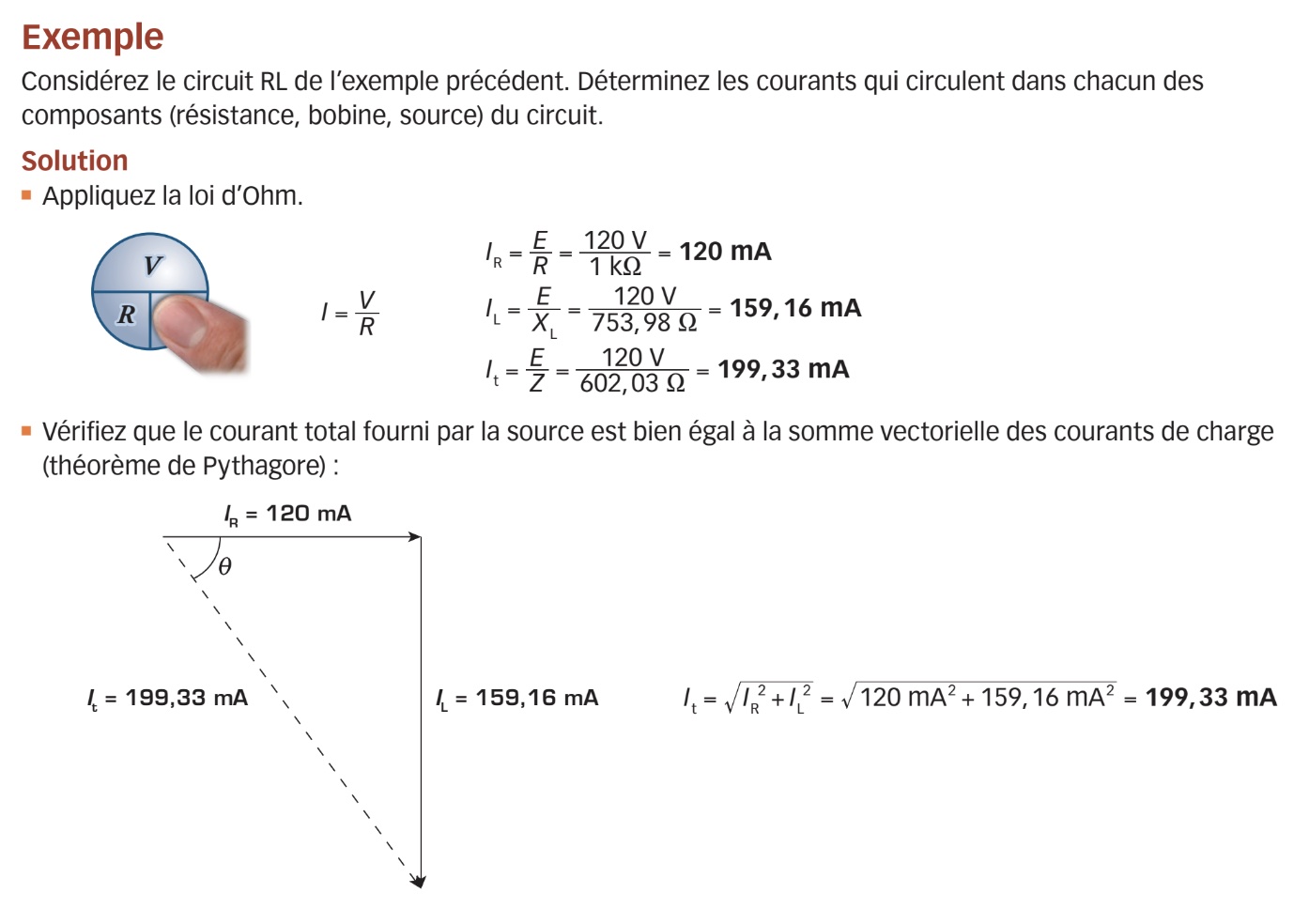
Déphasage entre le courant et la tension de source du circuit RL en parallèle

Dans l’exemple précédent, le courant total (It) est déphasé par rapport à la tension de source (E). Ce déphasage est causé par l’effet que produit la bobine sur le courant. Comme la tension de source (E) est en phase avec le courant de la résistance (IR), il y a un angle de déphasage (i) entre le courant de la résistance (IR) et le courant de la source (It). Pour déterminer la valeur de cet angle de déphasage, on recourt à l’une des trois fonctions trigonométriques associées au triangle rectangle des courants (SOHCAHTOA). Dans ce cas, nous utiliserons la fonction du cosinus.

Comportement du condensateur en c.a.

À l’instar de la bobine, le condensateur ne se comporte pas dans un circuit c.a. comme il se comporte dans un circuit c.c. Son comportement en c.a. se rapproche aussi beaucoup de celui de la résistance. Bien que le condensateur soit toujours caractérisé par sa capacité (C), de nouveaux concepts sont utilisés pour analyser son fonctionnement dans un circuit alimenté en c.a. Ces concepts sont similaires à ceux relatifs à la bobine, mais, d’une certaine façon, ils sont tous inversés.

Réactance capacitive

Le comportement d’un condensateur alimenté en courant alternatif est caractérisé par la réactance capacitive, qui traduit l’opposition exercée par le condensateur au passage du courant alternatif. La réactance capacitive est représentée par XC, et on la mesure en ohms (Ω). La réactance capacitive d’un condensateur peut être déterminée par la formule suivante :

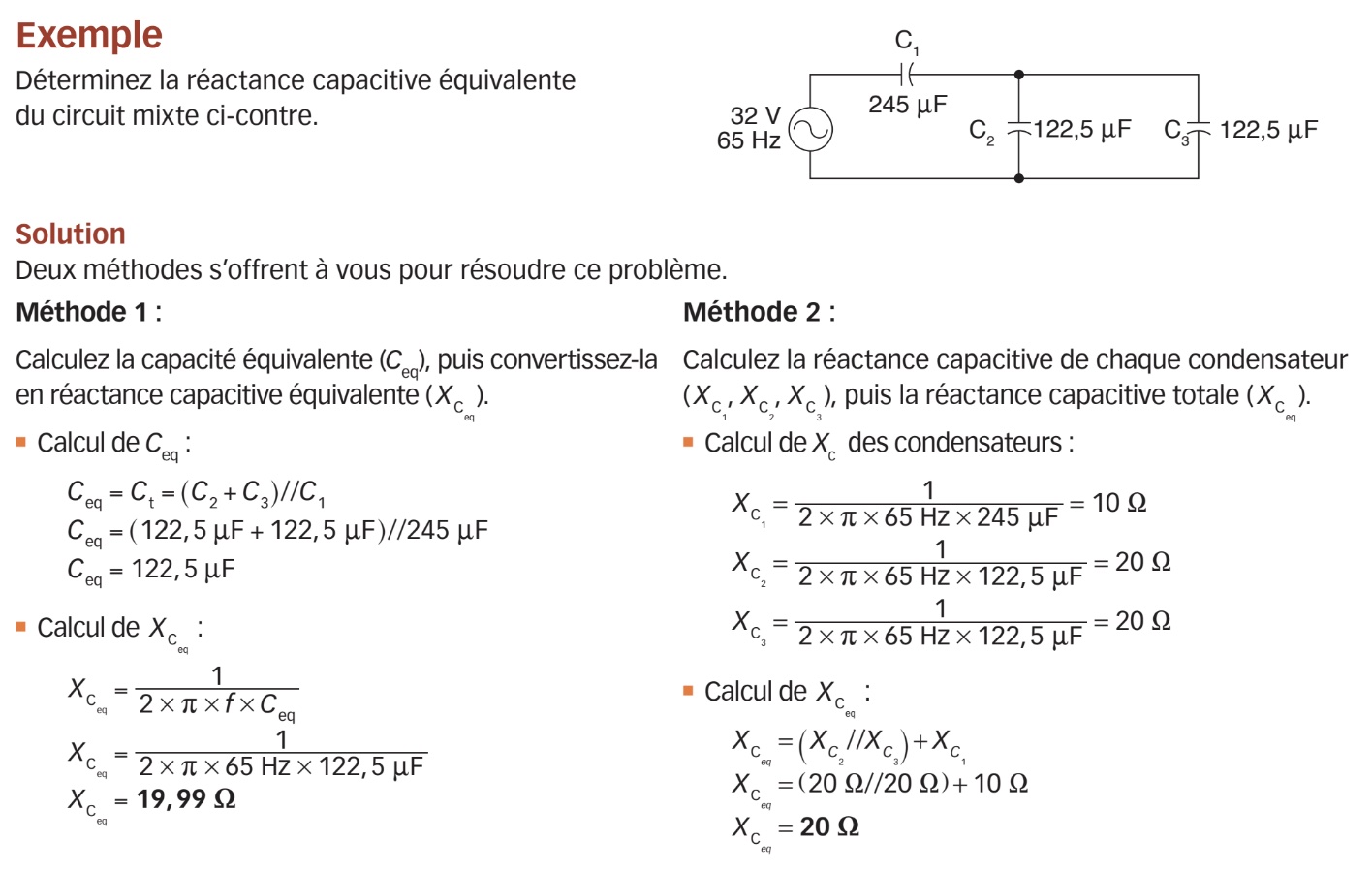
Réactance capacitive équivalente

Tout d’abord, souvenez-vous que le calcul de la capacité équivalente ou totale d’un agencement de condensateurs est souvent une cause d’erreur. Le calcul de la capacité équivalente de condensateurs se fait selon le principe inverse du calcul de la résistance équivalente (et aussi de celui de l’inductance équivalente). Ainsi, la capacité équivalente d’un agencement de condensateurs reliés en série se calcule comme on calcule la résistance équivalente de résistances reliées en parallèle, et vice versa.

Ces affirmations restent vraies lorsqu’il s’agit de courant alternatif, et la réactance capacitive équivalente ou totale d’un circuit peut donc être déterminée à partir de la capacité équivalente (C eq) en utilisant la formule suivante :

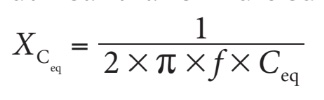
Déphasage de la tension

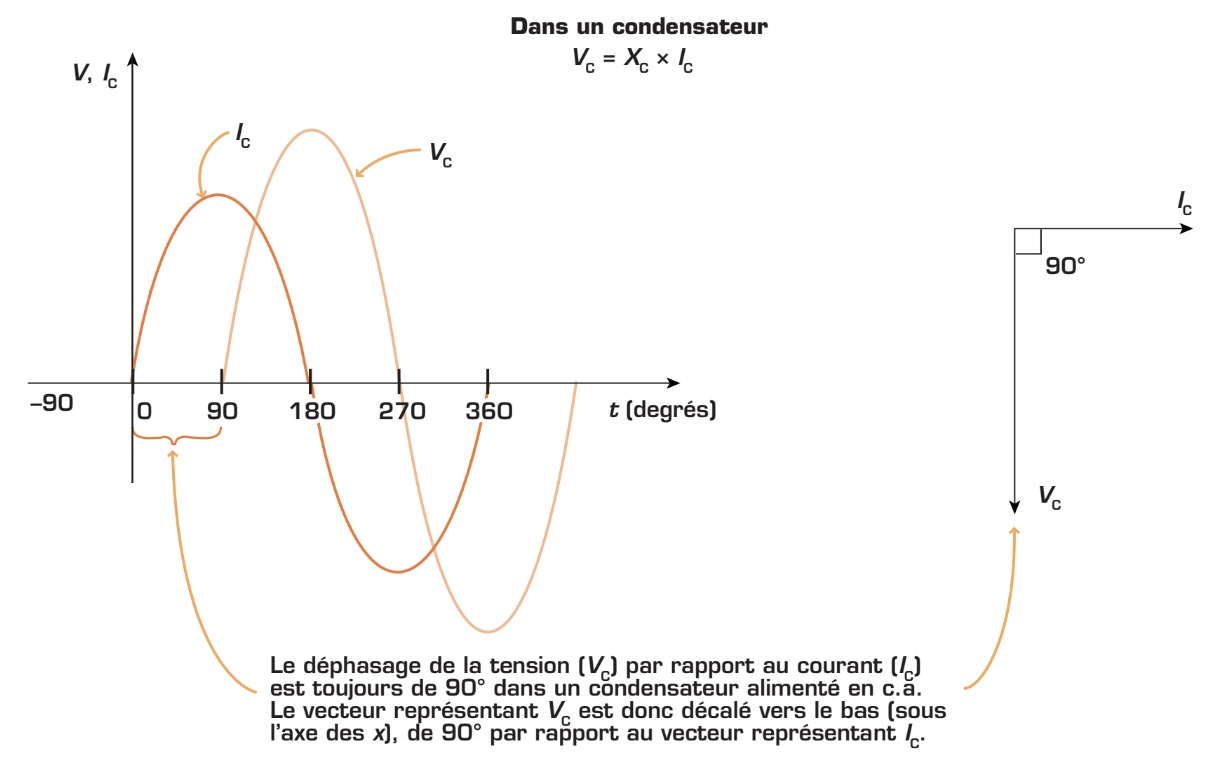
Comme la bobine, le condensateur entraîne un déphasage dans le circuit c.a. entre le courant et la tension à ses bornes. Toutefois, contrairement à ce qui se produit dans le cas de la bobine, c’est la tension aux bornes du condensateur (VC) qui est en retard de phase de 90° par rapport au courant (IC). Ce phénomène s’explique par le fait que le condensateur s’oppose aux variations de la tension dans le circuit. La figure qui suit montre la relation de phase entre ces deux paramètres.

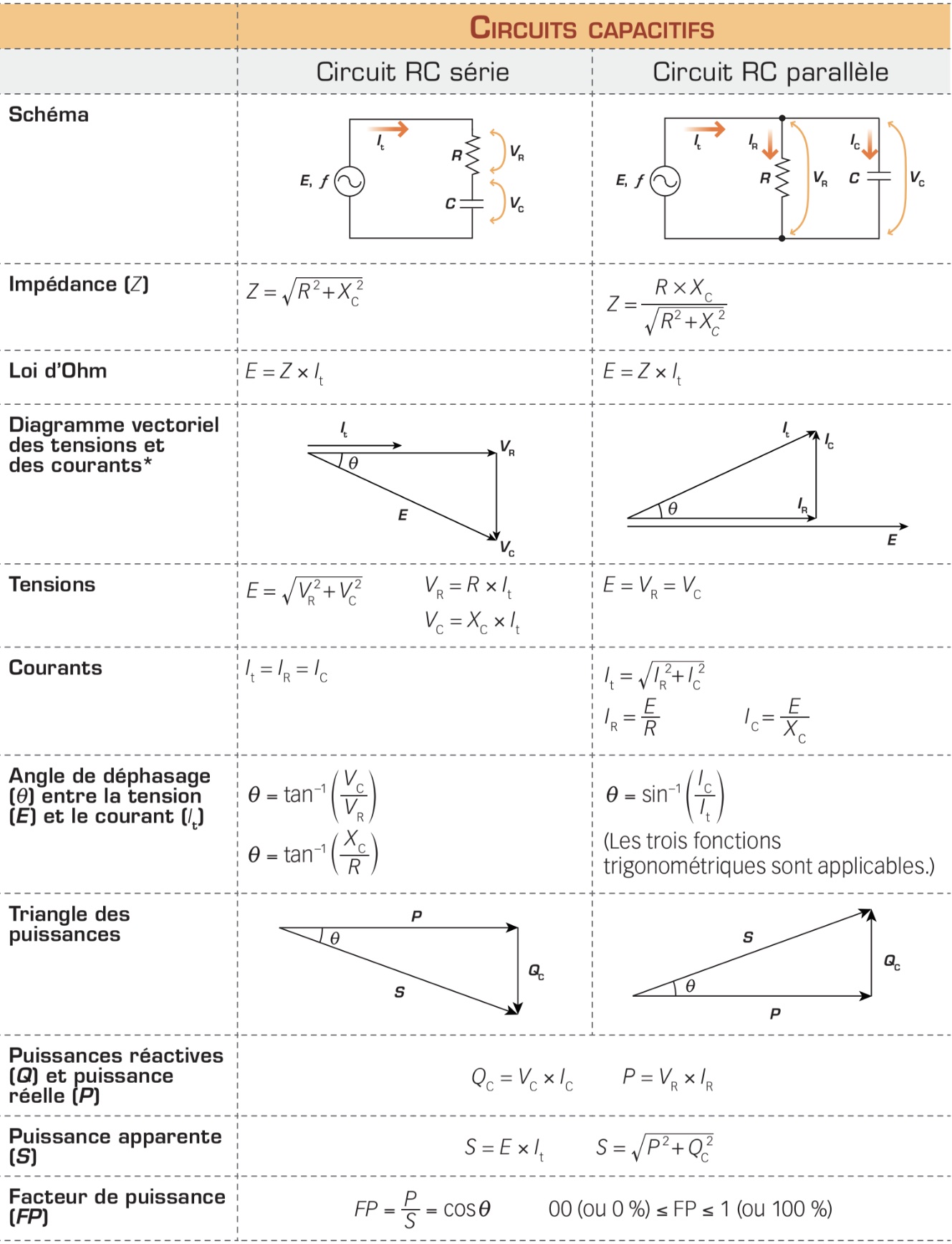
Circuits capacitifs RC

Contrairement aux résistances et aux bobines qui sont intégrées dans de nombreux dispositifs électriques, les condensateurs sont habituellement utilisés dans les circuits industriels. Ainsi, des condensateurs sont souvent installés dans les composants d’alimentation des circuits industriels afin d’en améliorer la performance. Étudions l’interaction entre un condensateur et une résistance dans un circuit RC alimenté en c.a., selon la configuration de l’agencement.

Circuit RC série

L’étude des circuits RC série est similaire à celle des circuits RL série, mais les principes y sont inversés.

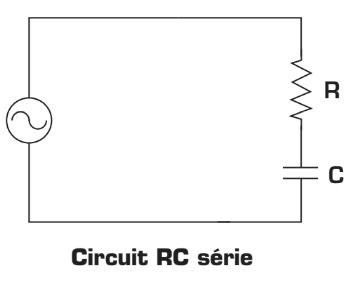
Impédance du circuit RC série

Vous savez maintenant que l’impédance représente l’opposition totale du circuit au passage du courant alternatif (et qu’elle correspond à la résistance équivalente d’un circuit résistif). L’impédance est cette fois encore représentée par Z et on la mesure en ohms (Ω).

Deux méthodes peuvent être utilisées pour déterminer l’impédance d’un circuit RC série, selon les paramètres connus.

Méthode 1 : Calcul de l’impédance à l’aide de la loi d’Ohm

Méthode 2 : Calcul de l’impédance à partir d’un diagramme vectoriel

Si vous connaissez la valeur de la résistance et de la réactance capacitive du circuit, vous pouvez déterminer la valeur de l’impédance en élaborant le diagramme vectoriel de l’impédance. Comme dans le cas de la bobine, faites bien attention de ne pas additionner directement la valeur de la résistance avec celle de la réactance capacitive. L’exemple suivant vous montre la marche à suivre.

Courant du circuit RC série

Tout comme dans les circuits RL, on calcule le courant total d’un circuit RC à l’aide de la loi d’Ohm, en n’oubliant pas d’utiliser l’impédance comme valeur de résistance.

Tensions du circuit RC série

Puisque nous sommes en présence d’un circuit série, la tension de source se divise entre chacune des charges (soit la résistance R et le condensateur C) proportionnellement à la résistance (R) et à la réactance capacitive (XC). Cependant, en raison du déphasage de 90° entre la tension de source (E) et la tension du condensateur (VC), cette répartition de la tension se fait vectoriellement. En d’autres termes, la tension de la source (E) est égale à la somme vectorielle de la tension aux bornes de la résistance (VR) et de celle aux bornes du condensateur (VC). La figure qui suit montre la relation entre le courant (qui est partout le même, car c’est un circuit série) et les différentes tensions du circuit.

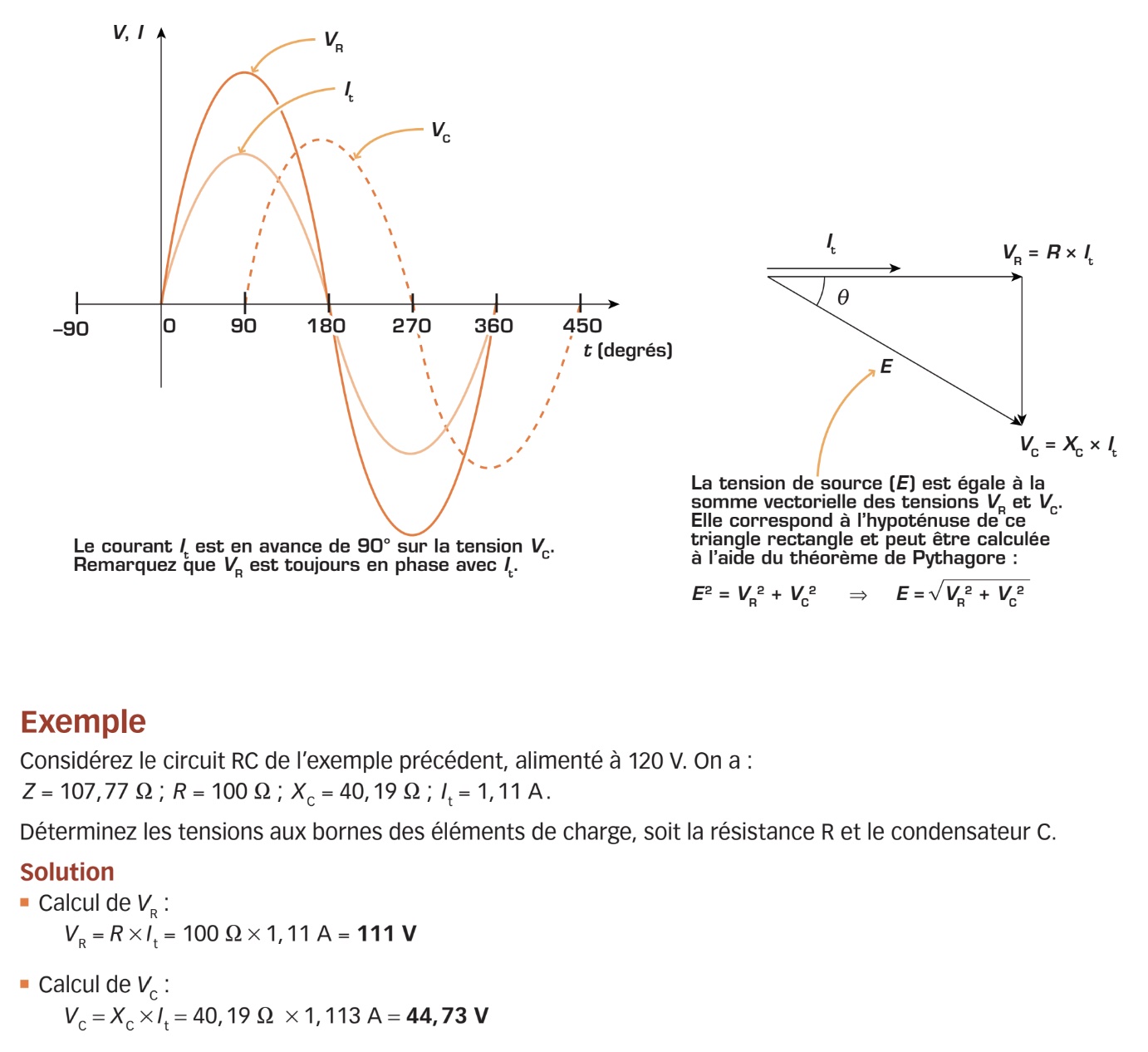
Déphasage entre le courant et la tension de source du circuit RC série

Le diagramme vectoriel illustré plus-haut montre un angle qui représente le déphasage entre la tension de la source (E) et le courant (It) débité par cette dernière. La valeur de cet angle peut être déterminée, par exemple, en utilisant la fonction trigonométrique de la tangente :

Circuit RC parallèle

La très grande majorité des condensateurs qui sont installés dans les circuits industriels sont reliés en parallèle avec la source d’alimentation. Dans ce type de circuit, la tension est commune aux bornes de tous les éléments, et le courant se divise selon la résistance ou la réactance de chaque charge.

Impédance du circuit RC parallèle

Comme pour la bobine, il existe deux méthodes pour déterminer l’impédance (Z) d’un circuit RC en parallèle, selon les paramètres connus.

Méthode 1 : Calcul de l’impédance à l’aide de la loi d’Ohm Si vous connaissez la valeur de la tension (E) et du courant (It) du circuit, vous pouvez appliquer la loi d’Ohm en remplaçant la valeur de la résistance (R) par celle de l’impédance (Z).

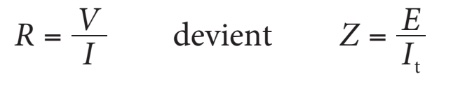
Méthode 2 : Calcul de l’impédance d’un circuit RC parallèle

Si vous connaissez la valeur de la résistance (R) et celle de la réactance capacitive (XC) du circuit, vous pouvez également déterminer la valeur de l’impédance totale (Z) d’un circuit RC en parallèle. Toutefois, comme dans le cas des circuits RL en parallèle, vous devez utiliser une formule spéciale spécifique :

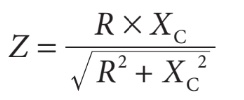
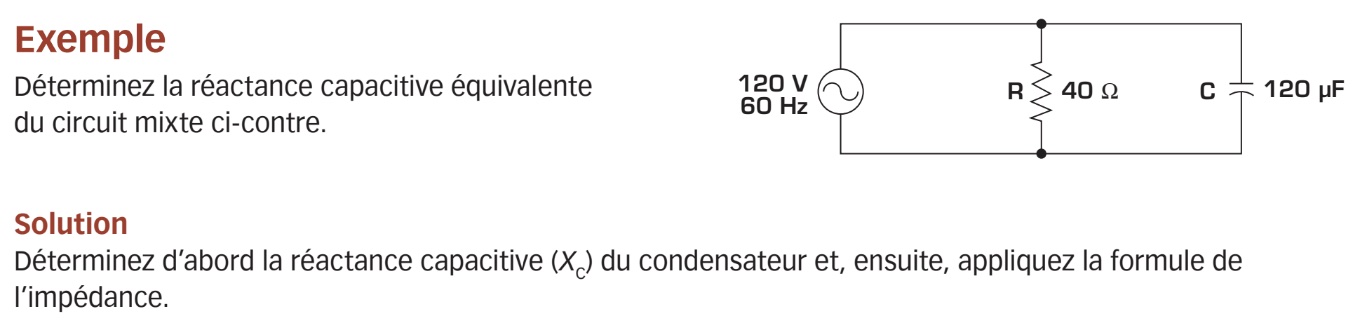
Courants du circuit RC parallèle

Vous savez déjà que plusieurs courants différents circulent dans les circuits en parallèle. Voici les particularités des courants dans un circuit RC parallèle :

le courant qui traverse la résistance (IR) est en phase avec la tension de source (E);
le courant du condensateur (IC) est en avance de 90° par rapport à la tension de source (E);
le courant total fourni par la source (It) est en avance sur sa tension (E) d’un angle de 0° à 90°, selon la répartition entre R et XC.

Observez ci-dessous le diagramme vectoriel correspondant aux relations entre ces trois courants et la tension de source (E).

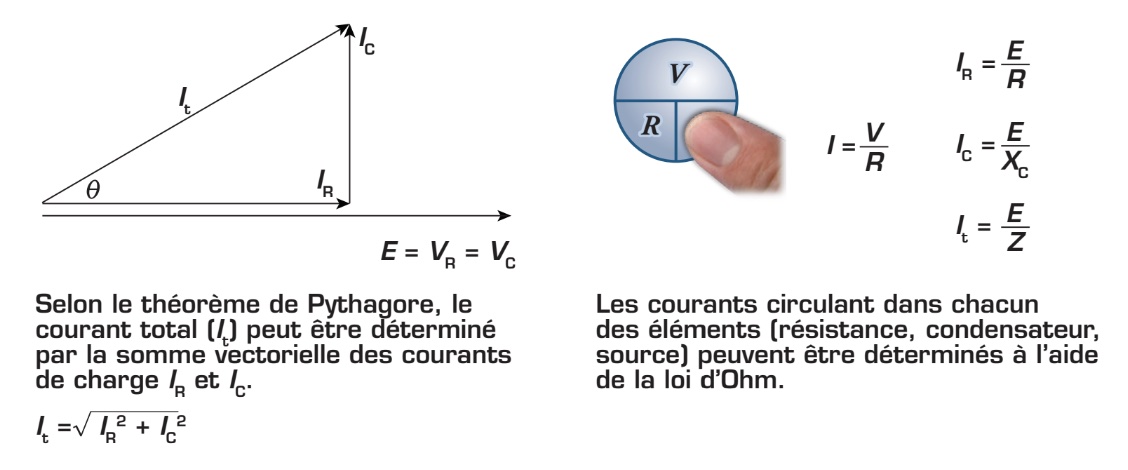
Déphasage entre le courant et la tension de source du circuit RC en parallèle

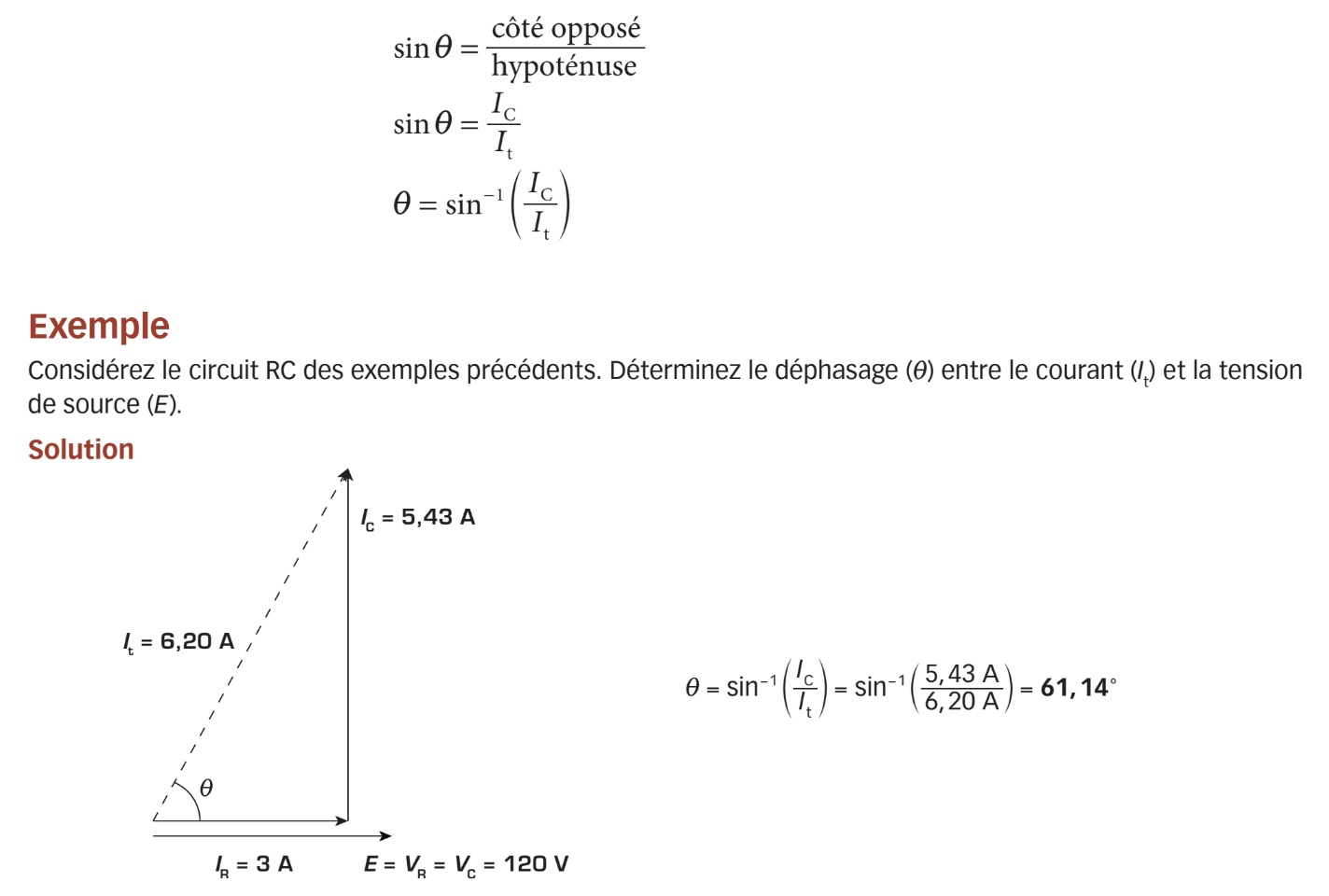
Étant donné que la résistance n’entraîne pas de déphasage et que les éléments sont reliés en parallèle, nous pouvons affirmer que la tension de source (E) est en phase avec le courant qui traverse la résistance (IR). Le déphasage (i) entre la tension de source (E) et le courant de source (It) correspond donc à l’angle formé par les vecteurs des courants IR et It. Pour déterminer cet angle, il suffit d’appliquer une des fonctions trigonométriques associées à un triangle rectangle (SOHCAHTOA). Dans ce cas, nous utiliserons la formule trigonométrique du sinus.

Puissances et facteur de puissance

L’étude des circuits alternatifs et des différents éléments de charge amène l’utilisation de nouveaux concepts de puissance. Examinons-les en détail.

Puissance réactive

Vous avez vu que les bobines et les condensateurs ne consomment pas d’énergie puisqu’ils restituent à la source la même quantité d’énergie qu’ils absorbent. On parle donc plutôt d’échange d’énergie au lieu de consommation d’énergie. C’est pourquoi l’expression puissance réactive est utilisée pour désigner la puissance échangée par ces composants. Cette puissance est représentée par les symboles QL dans le cas d’une bobine et QC dans le cas d’un condensateur. Afin de la distinguer de la puissance réelle, exprimée en watts (W), on mesure la puissance réactive en vars (VAr); le nom de cette unité vient de l’abréviation des mots voltampère réactif.

Peu importe le type du circuit, la puissance réactive (Q) est toujours le produit de la tension présente aux bornes de l’élément réactif (bobine ou condensateur) multipliée par le courant circulant dans l’élément.

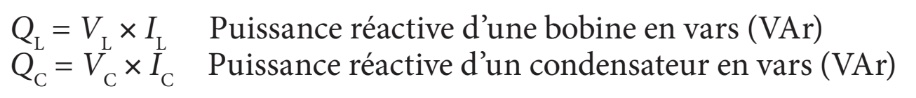
Pour bien distinguer les puissances réactives, on appelle aussi celle qui est associée à une bobine «puissance réactive inductive» et celle qui est associée à un condensateur «puissance réactive capacitive».

Puissance réelle

Contrairement à la bobine ou au condensateur, la résistance transforme l’énergie qu’elle absorbe en chaleur. Elle ne restitue donc aucune énergie à la source. Cette quantité d’énergie est alors appelée puissance réelle (ou puissance active). Elle est symbolisée par les lettres P ou PR, et elle se mesure en watts (W).

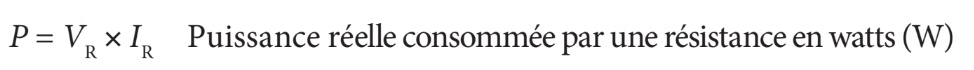
Puissance apparente

Pour pouvoir répondre à la demande de puissance de tous les éléments du circuit, la source doit fournir une puissance capable de satisfaire la demande en puissance réelle et celle en puissance réactive. Cette puissance totale fournie à la charge est appelée puissance apparente. Symbolisée par la lettre S, elle se mesure en voltampères (VA) et correspond au produit de la tension de la source (E) multipliée par son courant (It).

Dans les formules des trois types de puissances, les valeurs de tension et de courant correspondent aux valeurs efficaces.

Symbolisation des puissances

Graphiquement, la relation entre les trois types de puissances, apparente, réelle et réactive, peut être représentée par un triangle appelé « triangle des puissances ». L’orientation des triangles diffère selon le type et la configuration du circuit. Puisque les puissances sont le produit du courant et de la tension, l’orientation du triangle des puissances dépend de l’angle du déphasage entre la tension et le courant de source.

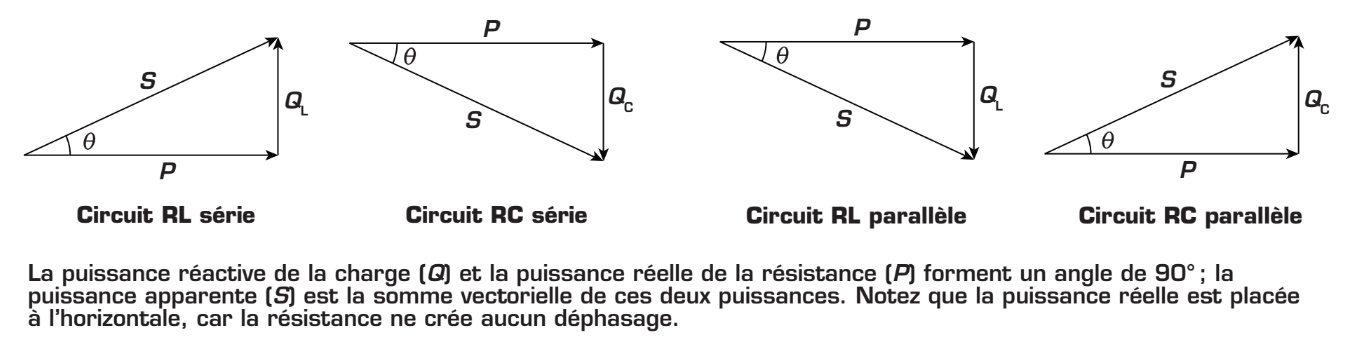
Comme vous pouvez le constater, ce triangle des puissances est un triangle rectangle. Ainsi, les formules usuelles du théorème de Pythagore et de la trigonométrie sont applicables. La puissance apparente (S) peut donc être exprimée par la formule suivante :

Facteur de puissance

Le facteur de puissance est la mesure du rendement de la puissance d’un circuit. Le facteur de puissance (FP) est le rapport entre la puissance réelle (P) consommée par le circuit et la puissance apparente (S) demandée à la source. Sans unité de mesure, le facteur de puissance peut également être exprimé en pourcentage (%).

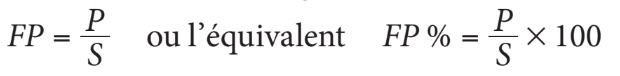
Le facteur de puissance est donc compris entre 0 (circuit purement réactif sans résistance : P = 0) et 1 ou 100 % (circuit purement résistif sans charge réactive : P = S). Il traduit, en quelque sorte, la «performance énergétique» d’un circuit. En effet, plus il s’approche de 1 ou 100 %, plus le travail de la source est utile, car une plus grande part de l’énergie demandée à la source est transformée en travail. Dans la pratique, il est donc souhaitable que le facteur de puissance d’un circuit électrique soit le plus près possible de 1 ou de 100 %.

Résumé

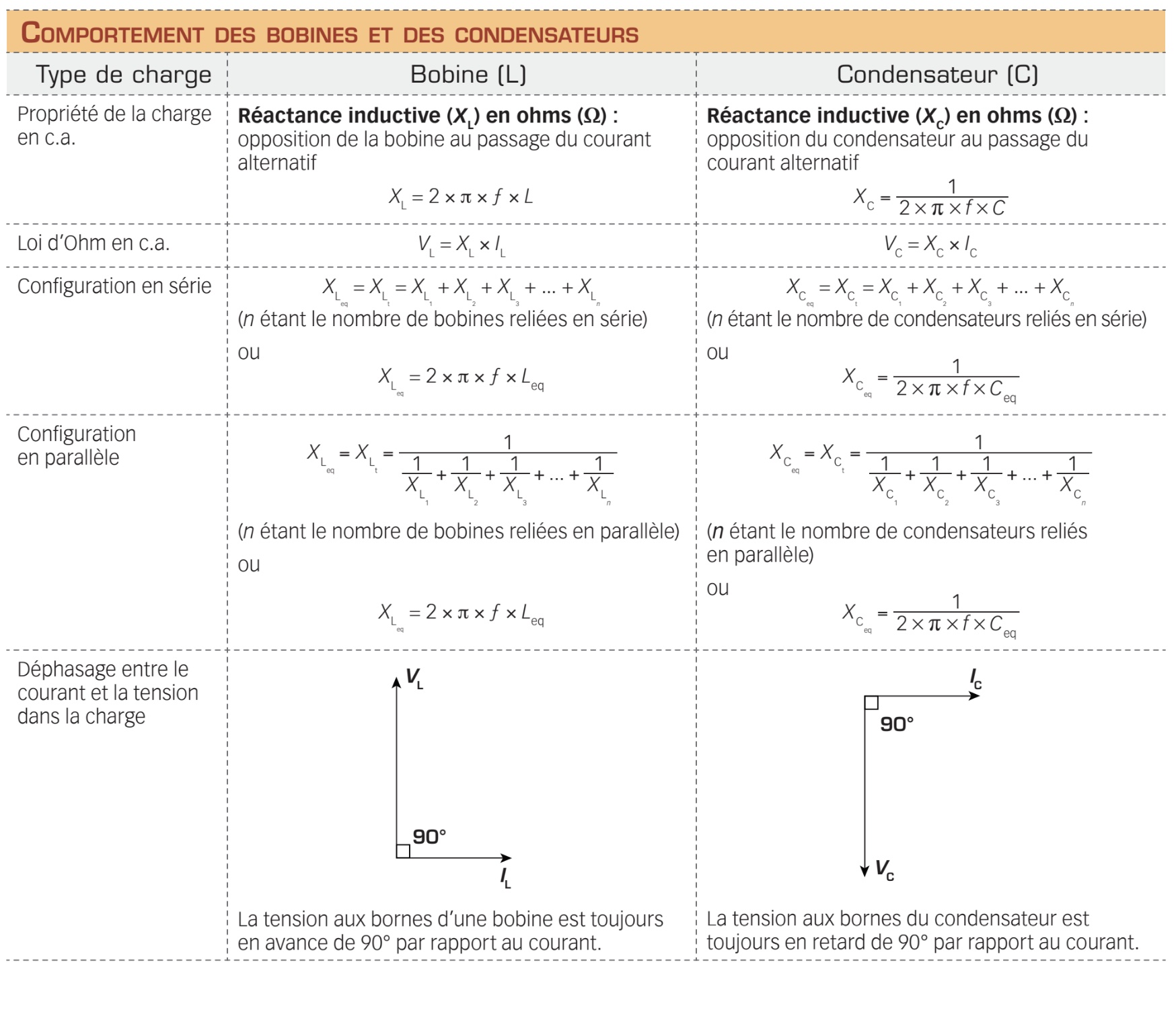
Dans les circuits alimentés en c.a., les charges réactives, inductives (bobines) et capacitives (condensateurs) se comportent en s’opposant aux variations du courant alternatif. Le tableau ci-dessous résume les principales caractéristiques des bobines et des condensateurs dans les circuits c.a.

Dans la pratique, les charges réactives sont généralement associées à une charge résistive (résistance) pour former des circuits réactifs RL (bobine + résistance) ou RC (condensateur + résistance). Le second tableau présente les principales notions qui permettent de distinguer les circuits RL et RC alimentés en c.a., selon leur configuration (en série ou en parallèle). Notez que les circuits RL en parallèle sont les plus répandus.